集合の基礎の最後に、補集合に関して学んでいきます。
・全体集合と補集合
集合を考えるときは、実数・正の数・整数などのようにあらかじめある範囲を設定し(もしくは問題文でされていて)、その範囲の中で議論をしていくことが多いです。つまりもとの設定する(全体の)集合を\(U\)として、その部分集合\(A,B,C・・・\)を考えていくわけです。このとき\(U\)を全体集合といいます。
\(A\)が全体集合\(U\)の部分集合であるとき、\(U\)の要素は\(A\)に属するものと属さないものに分かれます。\(U\)の要素であって、\(A\)に属さない要素全体が作る集合を\(U\)に関する補集合といい、\(\overline{A}\) で表します。つまり、
\(\overline{A}=\{x|x\in U\) かつ \(x\notin A\}\)
となります。
(例)
\(U=\{1,2,3,4,5,6\}\), \(A=\{2,4,6\}\) とすると
\(\overline{A}=\{1,3,5\}\)
ベン図で全体集合\(U\)と集合\(A\)と補集合\(\overline{A}\)は次のように表されます。
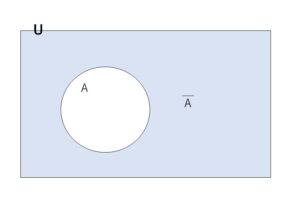
この図から次の性質が成り立つことがわかります。
②\(A \cap \overline{A}=φ\)
③\(\overline{\overline{A}}=A\)
④\(\overline{U}=φ\)
⑤\(\overline{φ}=U\)
→④については、\(U\)の要素の中に\(U\)に属さないものはないので、\(\overline{U}=φ\) となり、⑤については空集合には要素がないので、\(U\)の要素の中で集合\(φ\)に属さないものは\(U\)の要素全てとなるので、⑤が成り立つ。
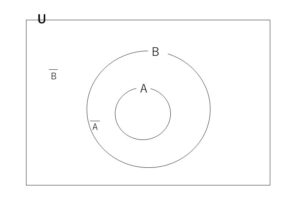
ベン図を用いると次の法則(ド・モルガンの法則)が成り立つことがわかります。
②\(\overline{A \cup B}\)\(=\overline{A} \cap \overline{B}\)
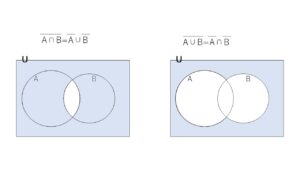
少しだけ演習をします。
(問題1)
実数全体を全体集合とし、\(A=\{x|0<x<6\}\), \(B=\{x|x<-2,2<x\}\), \(C=\overline A \cup \overline B\)とする。\(C\)を求めよ。
(解答)
\(\overline A=\{x|x≦0,x≧6\}\),
\(\overline B=\{x|-2≦x≦2\}\) だから
\(C=\{x|x≦2,x≧6\}\)
(問題2)
全体集合\(U\)を\(10\)以下の自然数として、\(U\)の部分集合\(A,B\)を、
\(A=\{1,2,4,6,8\}\) \(B=\{1,3,6,9\}\) とするとき、\(\overline{\overline A \cup B}\)を求めよ。
(解答)
ド・モルガンの法則より
\(\overline{\overline A \cup B}\)\(=\overline{\overline A} \cap \overline B\)\(=A \cap \overline B\)
\(\overline B\)\(=\{2,4,5,7,8,10\}\) だから
\(\overline{\overline A \cup B}\)\(=A \cap \overline B=\)\(\{2,4,8\}\)
(問題3)
\(1\)以上\(100\)以下のすべての整数の集合\(U\)を全体集合として考える。
\(A=\{x|x\)はある整数の平方 \(,x \in U\}\)
\(B=\{x|x\)は偶数 \(,x \in U\}\)
\(C=\{x|x\)は\(4\)の倍数 \(,x \in U\}\) とするとき
(1)集合 \(A \cap B\) を要素を書き並べて表せ。
(2)\(\overline C \subset \overline A \cup \overline B\) であることを示せ。
(解答)
(1)
\(A=\{1,4,9,16,25,\)\(36,49,64,81,100\}\) だから、
\(A \cap B=\)\(\{4,16,36,64,100\}\)
(2)
\(C \supset A \cap B\)となる。よって
\(\overline C \subset \overline {A \cap B}\)
また、ド・モルガンの法則より
\(\overline C \subset \overline A \cup \overline B\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。