(2-1,2-2)の2つの集合、3つの集合の要素の個数の知識を駆使して、倍数の個数の問題を解いていきます。
(問題1)
100以上200以下の自然数で、次のような数はいくつあるか。
(1)2または3で割り切れる数
(2)2で割り切れるが、3では割り切れない数
2の倍数の個数は、100(2×50) から 200(2×100) まで考えるから、100-50=50個としたら間違いです。例えば最初の3つの数を考えてみると、 100(2×50) 102(2×51) 104(2×52) なので、その個数は 3=(52-50)+1 です。 よって100から200までの2の倍数の個数は 100ー50+1=51個 となります。
(解答)
(1)
2,3で割り切れる数の集合をそれぞれ\(A,B\)とする。
\(A=\{2×50,2×51,・・・,2×100\}\) だから
\(n(A)=100-50+1=51\)
\(B=\{3×34,3×35,・・・,3×66\}\) だから
\(n(B)=66-34+1=33\)
\(A \cap B=\{6×17,6×18,・・・6×33\}\) より
\(n(A \cap B)=33-17+1=17\)
求める個数は、\(n(A \cup B)\)個だから
\(n(A \cup B)\)\(=n(A)+n(B)-n(A \cap B)\)\(=51+33-17=\)\(67(個)\)
(2)
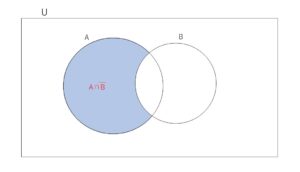
求める個数は、\(n(A \cap \overline B)\)個
図より
\(n(A \cap \overline B)\)\(=n(A)-n(A \cap B)\)\(=51-17=\)\(34(個)\)
(問題2)
1000以下の自然数について、次の数の個数を求めよ。
(1)4でも6でも9でも割り切れる数
(2)4では割り切れるが、6でも9でも割り切れない数
(解答)
(1)
4でも6でも9でも割り切れる数の集合は、\(A \cap B \cap C\)であり、それは36で割り切れる数の集合である。よって
\(A \cap B \cap C\)\(=\{36×1,36×2,・・・,36×27\}\)
\(n(A \cap B \cap C)=\)\(27(個)\)
(2)
こういう間違いを無くすためにはやはりベン図を考えた方がよいでしょう。
\(A=\{4×1,4×2,・・・,4×250\}\) より
\(n(A)=250\)
\(A \cap B\)は4でも6でも割り切れる数の集合なので
\(A \cap B=\)\(\{12×1,12×2,・・・,12×83\}\) より
\(n(A \cap B)=83\)
\(A \cap C\)は4でも9でも割り切れる数の集合なので
\(A \cap C=\)\(\{36×1,36×2,・・・,36×27\}\) より
\(n(A \cap C)=27\)
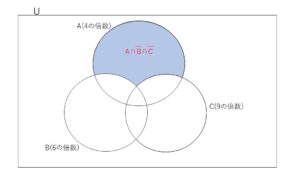
求める個数は\(n(A \cap \overline B \cap \overline C)\)個なので、図より
\(n(A \cap \overline B \cap \overline C)\)\(=n(A)-n(A \cap B)-n(A \cap C)+n(A \cap B \cap C)\)
\(=250-83-27+27=\)\(167(個)\)
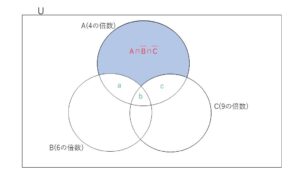
図のように各領域の集合の要素の個数を\(a,b,c\)と設定すると、
\(n(A \cap B)=a+b\) で、\(n(A \cap B)\)は上の方法と同じように83、\(b\)は\(n(A \cap B \cap C)\)だから(1)より\(b=27\)、よって \(a=83-27=56\)
\(n(A \cap C)=b+c\) で、\(n(A \cap C)\)は上の方法と同様に27だから、\(c=27-27=0\)
よって、(求める個数)\(=n(A)-(a+b+c)\)\(=250-(56+27+0)\)\(=167\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。