数列と等差数列の基本事項について見ていきます。
・数列
自然数である偶数を小さい順に並べると
\(2,4,6,8,10,12\cdots\)
という数の列になりますが、このような数を一列に並べたものを数列といいます。
数列を構成している各数を、数列の項とよび、最初の項から順に、第1項、第2項、第3項・・・といい、第\(n\)番目の項を第\(n\)項といい、特に第1項を初項ともよびます。
数列を一般的に表すには、文字に項の番号を添えて
\(a_1,a_2,a_3,\cdots,a_n,\cdots\)
のように書きます。またこの数列を \(\{a_n\}\) と書くこともあります。ここで、第\(n\)項\(a_{n}\)が\(n\)の式で表されるとき、\(a_n\)をこの数列\(\{a_n\}\)の一般項といい、例えば最初に挙げた自然数の偶数で作られた数列の一般項は \(a_{n}=2n\) (\(n\)は自然数) となります。そしてこのように \(a_n=2n\) と\(n\)の式で得られると、\(n=1,2,3,\cdots\) を代入することにより、数列の各項を求めることができます。
自然数の偶数を数が小さい順に5つだけ並べた数列
\(2,4,6,8,10\)
のように、項の個数が有限である数列を有限数列といいます。有限数列では、項の個数を項数、最後の項を末項とよびます。
また、自然数の偶数をすべて並べた数列のように、項の個数が有限でない数列を無限数列とよびます。
まずは等差数列について見ていきます。
・等差数列
3で割って2余る自然数を小さい順に並べた数列は
\(2,5,8,11,14,17,\cdots\)
となりますが、この数列は
「2で始まり、前の項に3を加える」
という規則性で作られています。このように各項に一定の数\(d\)を加えると次の項が得られるような数列を等差数列といい、\(d\)をこの等差数列の公差といいます。等差数列は1つ前の項との差が一定である数列ともみることができます。そして、隣り合う2つの項 \(a_n,a_{n+1}\) の間に次の関係が成り立ちます。
\(a_{n+1}=a_n+d\) (前の項に\(d\)を加える)
つまり
\(a_{n+1}-a_n=d\) (差が\(d\)で一定)
次に等差数列の一般項がどうなるかを考えていきます。
数列\(\{a_n\}\)を「初項\(a\)、公差\(d\)の等差数列」とするとき
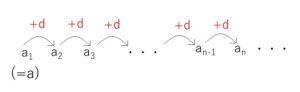
\(a_1=a\)
\(a_2=a+d=a+(2-1)d\)
\(a_3=a+2d=a+(3-1)d\)
\(a_4=a+3d=a+(4-1)d\)
\(・・・\)
より、第\(n\)項\(a_{n}\)は初項\(a\)に公差\(d\)を\(n-1\)回加えたものになるから、一般項は次のようになります。
\(a_n=a+(n-1)d\)
分からなくなったら\(n=1\)を代入して \(a_1=a+(1-1)d=a\) となることで確認してください。
(例題1)
等差数列 \(\{a_n\}\) において、
\(a_{10}-a_{6}=8\), \(5a_{3}=7a_{2}\)
である。
(1)等差数列\(\{a_n\}\)の一般項を求めよ。
(2)\(a_{11}+a_{12}+a_{13}\)を求めよ。
(3)\(a_{n-2}+a_{n-1}+a_{n}\) (\(n=3,4,5,\cdots\)) の値が\(3000\)を超える最小の\(n\)の値を求めよ。
(解答)
(1)
条件式2つから、\(a,d\)を決定していきます。
\(a_{n}=a+(n-1)d\) とおくと
\(a_{10}-a_{6}=8\), \(5a_{3}=7a_{2}\) より
\(a+9d-(a+5d)=8\)・・・①
\(5(a+2d)=7(a+d)\)・・・②
①より \(d=2\)
これと②より \(a=3\)
したがって
\(a_n=3+2(n-1)\)
\(=2n+1\)
(2)
\(a_{11}+a_{12}+a_{13}\)
\(=(2\cdot11+1)+(2\cdot12+1)+(2\cdot13+1)\)
\(=75\)
(3)
\(a_{n-2}+a_{n-1}+a_{n}\)
\(=\{2(n-2)+1\}+\{2(n-1)+1\}+(2n+1)\)
\(=6n-3\)
よって
\(6n-3>3000\) だから
\(n>500.5\)・・・③
③を満たす最小の\(n\) (\(3\)以上の自然数) は
\(n=501\)
(例題2)
\(k\)を\(0\)でない定数として、一般項が \(a_n=k(n-1)\) である数列\(\{a_n\}\)について、\(b_{n}=a_{4n}\) で表される数列\(\{b_n\}\)は等差数列であることを証明し、初項と公差を求めよ。
(解答)
\(b_n=a_{4n}\)
\(=k(4n-1)\)
\(=4kn-k\)
\(b_{n+1}-b_{n}\)
\(=4k(n+1)-k-(4kn-k)\)
\(=4k\)
\(=(一定)\)
したがって、\(b_n\)は公差\(4k\)の等差数列である。
また初項については、\(b_1=4k-k=\)\(3k\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→等差数列をなす3数