等差数列の和の最大値

等差数列の和の最大値に関する例題です。

(例題1)
等差数列 \(51,47,43,\cdots\) の初項から第\(n\)項までの和を\(S_n\)とする。\(S_n\)は \(n=\)(　) のとき最大になり、そのときの\(S_n\)の値は(　)である。また、\(|S_n|\) は、\(n=\)(　) のときに最小になる。

(解答)
この等差数列\(\{a_n\}\)の一般項は
\(a_n=51-4(n-1)=-4n+55\)

よって
\(S_n=\displaystyle\frac{1}{2}n\{51+(-4n+55)\}\)

\(=-2n^2+53n\)

\(=-2(n-\displaystyle\frac{53}{4})^2+\displaystyle\frac{53^2}{8}\)

\(S_n\)を2次関数とみると、\(\displaystyle\frac{53}{4}=13.25\) だから
最大値は \(n=13\)  のとき
\(S_{13}=-2\cdot13^2+53\cdot13\)\(=351\)

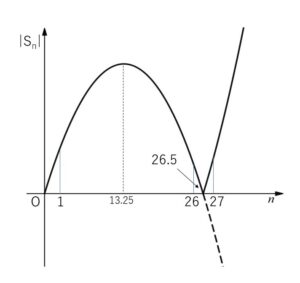
また
\(|S_n|=|-2n^2+53n|\)\(=|n(-2n+53)|\) であり
\(\displaystyle\frac{53}{2}=26.5\) より、\(|S_n|\)のグラフを考えると、最小となるときの候補は、\(|S_1|,|S_{26}|,|S_{27}|\)

\(|S_1|=|51|=51\)
\(|S_{26}|=|26|=26\)
\(|S_{27}|=|-27|=27\)

したがって\(|S_n|\)は \(n=26\) のとき最小になる。

(\(S_n\)が最大となる\(n\)の値)

等差数列\(\{a_n\}\)は、\(51\)スタートでどんどん減っていく数列です。
項の値が\(0\)以上である限りは、加えていくことで和はどんどん大きくなっていくので、\(S_n\)が最大となるのは\(a_n\)が\(0\)以上となる最後の項まで加えたときです。(ちょうど\(0\)になる項があれば最大値をとる\(n\)は2つ存在する)

よって
\(a_n=-4n+55≧0\) を解いて
\(n≦13.75\)

したがって \(a_{1}～a_{13}>0\) で、\(a_{14}～<0\) となるので、\(S_n\)が最大となるときの\(n\)は\(n=13\) となることが分かります。

(例題2)
数列 \(a_1,a_2,\cdots,a_n,\cdots\) は、初項\(a\)、公差\(d\)の等差数列であり、\(a_3=12\) かつ、\(S_8>0\), \(S_9≦0\) を満たす。ただし、\(S_n=a_1+a_2+\cdots+a_n\) である。

(1)公差\(d\)がとる値の範囲を求めよ。
(2)\(a_n\) (\(n>3\)) がとる値の範囲を、\(n\)を用いて表せ。
(3)\(a_n>0\), \(a_{n+1}≦0\) となる\(n\)の値を求めよ。
(4)\(S_n\)が最大となるときの\(n\)の値をすべて求めよ。また、そのときの\(S_n\)を\(d\)の式で表せ。

(解答)
(1)
\(a_n=a+(n-1)d\)

\(a_3=12\) より
\(a+2d=12\)・・・①

また
\(S_n=\displaystyle\frac{1}{2}n\{2a+(n-1)d\}\) だから

\(S_8>0\), \(S_9≦0\) より

\(4(2a+7d)>0\)・・・②
\(9(a+4d)≦0\)・・・③

(\(d\)の範囲が知りたいので、\(a\)を消去します)

①より \(a=12-2d\)
これを②③に代入して
\(4(24+3d)>0\)
\(9(12+2d)≦0\)

したがって
\(-8<d≦-6\)

(2)
\(a_n=a+(n-1)d\)
\(=12-2d+(n-1)d\)
\(=(n-3)d+12\)

\(n>3\) より \(n-3>0\) となるから、\(-8<d≦-6\) より
\(-8(n-3)+12<a_n≦-6(n-3)+12\)

したがって
\(-8n+36<a_n≦-6n+30\)

(3)

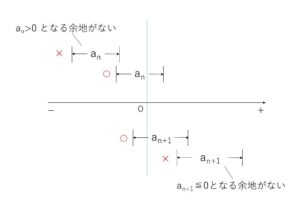
\(n>3\)のときは \(a_n\)の範囲は(2)で求めたとおりです。
まず、\(a_n>0\) についてですが、この範囲の中に正の値になるものが少なくとも存在していなくてはいけないので、範囲の右端である \(-6n+30>0\)・・・④ が条件(必要条件)となります。\(a_{n+1}≦0\) も同様に考えて左端について \(-8(n+1)+36<0\)・・・⑤ です。すると \(n=4\) のみが候補になりますが、④⑤はそれぞれ範囲の中に正のもの負のものがあるかどうかを確認しているだけなので、\(n=4\)のとき実際に条件をみたすかどうかの確認が必要です。また、\(n=1,2,3\)のときは別途考えて潰しておきます。なお④⑤の導き方については解答では数式で処理していきます。

\(a_3=12\)、\(-8<d≦-6\) より
\(a_1,a_2,a_3,a_4>0\) となるから
\(n=1,2,3\) のとき、\(a_n>0\), \(a_{n+1}≦0\) は満たさない。

よって\(n>3\)として(2)より
\(-6n+30≧a_n>0\)
\(-8(n+1)+36<a_{n+1}≦0\)

ゆえに
\(-6n+30>0\)・・・④
\(-8(n+1)+36<0\)・・・⑤

④⑤より
\(3.5<n<5\)

したがって\(n=4\)として
\(a_4=d+12>0\)　(\(∵d>-8\))
\(a_5=2d+12≦0\)　(\(∵d≦-6\))
であるから、\(n=4\)は条件を満たす。

(4)

(3)より

(i)\(-8<d<-6\) のとき
\(a_1,a_2,a_3,a_4\) は正の値で、\(a_5\)以降は負の値。
よって\(n=4\) のとき\(S_n\)は最大となり
\(S_4=\displaystyle\frac{1}{2}\cdot4\cdot\{24-4d+3d\}\)
\(=-2d+48\)

(ii)\(d=-6\)のとき
\(a_1,a_2,a_3,a_4\) は正の値で、\(a_5=0\)、\(a_6\)以降は負の値。
よって\(n=4,5\)のとき\(S_n\)は最大となり
\(S_4=-2d+48\)
\(=12+48\)
\(=60\)　(\(S_5\)も同じ)

まとめると
\(-8<d<-6\) のとき \(n=4\) で 最大値 \(-2d+48\)
\(d=-6\) のとき \(n=4,5\) で 最大値 \(60\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→既約分数の和　back→2つの数列の共通項