格子点の数を求める例題について見ていきます。
格子点の数を数える問題では、まず\(x,y\)の一方を固定して、縦 or 横 に数えてから最後に全体の個数を数えることになります。どちらを固定するかについては、境界線上が格子点になるかどうかなどに着目して簡単なほうを選ぶことになります。場合によっては偶奇で分けたりすることもあります。なお空間における格子点については(例題2)で扱います。
(例題1)
座標平面上で、\(x\)座標と\(y\)座標がともに整数である点を格子点という。\(n\)は自然数であるとして、不等式
\(x>0\), \(y>0\), \(\log_{2}\displaystyle\frac{y}{x}≦x≦n\)
をみたす格子点の個数を求めよ。
\(x≦n\) はこのままでよいので、\(\log_{2}\displaystyle\frac{y}{x}≦x\) について処理していきます。
(解答)
\(\log_{2}\displaystyle\frac{y}{x}≦x\) より
\(\log_{2}\displaystyle\frac{y}{x}≦x\log_{2}2\)
\(\log_{2}\displaystyle\frac{y}{x}≦\log_{2}2^{x}\)
底が\(2\)で\(1\)より大きいので
\(\displaystyle\frac{y}{x}≦2^{x}\)
\(x>0\) だから
\(y≦x\cdot2^{x}\)
よって
\(x>0\), \(y>0\), \(\log_{2}\displaystyle\frac{y}{x}≦x≦n\) は
\(0<x≦n\), \(0<y≦x\cdot2^{x}\) ・・・① となる。
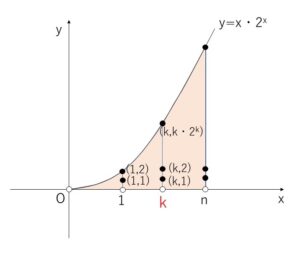
不等式①を満たす領域は、図の色付きの部分(\(x\)軸上は除く)である。\(x=k\)上の格子点の数は、\(y\)座標が \(1,2,3,\cdots,k\cdot2^{k}\) の値をとるので、\(k\cdot2^{k}\)個。
\(k\)は \(k=1,2,\cdots,n\) の値をとるから求める格子点の数\(S\)は
\(S=\displaystyle\sum_{k=1}^{n}k\cdot2^{k}\)
\(S=1\cdot2+2\cdot2^2+3\cdot2^{3}+\cdots+n\cdot2^{n}\)
\(2S=\hspace{24pt}1\cdot2^2+2\cdot2^3+\cdots+(n-1)\cdot2^n+n\cdot2^{n+1}\)
\(S-2S\) より
\(-S=2+2^{2}+2^{3}+\cdots+2^{n}-n\cdot2^{n+1}\)
\(-S=\displaystyle\frac{2(2^{n}-1)}{2-1}-n\cdot2^{n+1}\)
\(-S=2^{n+1}-2-n\cdot2^{n+1}\)
したがって
\(S=(n-1)2^{n+1}+2\)
(例題2)
\(xyz\)空間において、座標成分がすべて整数であるような点を格子点とよぶことにする。この空間における領域\(D\)を、次の不等式をみたす部分として定める。
\(x≧0\), \(y≧0\), \(z≧0\), \(x+y+z≦n\) (\(n\):正の整数)
(1)領域\(D\)を平面\(x=i\) (\(0≦i≦n\), \(i\)は整数) で切った切り口にある格子点の個数を\(i\)と\(n\)を用いて表せ。
(2)領域\(D\)に含まれる格子点の個数を\(n\)を用いて表せ。
(1)
\(y≧0\), \(z≧0\), \(i+y+z≦n\) (\(y+z≦n-i\))
となり、\(y,z\)座標(平面)で考えていくことなります。文字多いですが、固定した\(i\)は定数で、\(n\)も\(xyz\)空間では定数です。
\(x=i\) (\(0≦i≦n\), \(i\)は整数) のとき
\(y≧0\), \(z≧0\), \(z≦-y+n-i\)・・・①
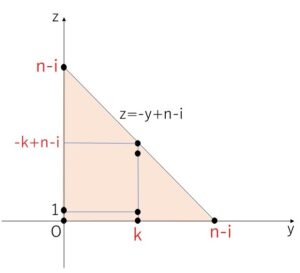
不等式①が表す領域は図の色付きの部分で、\(y=k\) (\(k=0,1,2,\cdots,n-i\)) のときの格子点の個数は、\(z\)が \(z=0,1,2,\cdots,(-k+n-i)\) の値をとるので、\((-k+n-i+1)\) 個。
また、\(z=0,1,2,\cdots\) と \(0\)スタートになっているので、例えば \(z=0,1,2,3\) では個数は\(4\)個で、これは \(3+1=4\) から求まることから1を加えることになります。
よって平面\(x=i\)で切った切り口の格子点の個数は
\(\displaystyle\sum_{k=0}^{n-i}(-k+n-i+1)\)
(変数は\(k\)、\(k=0\)スタートであることに注意して)
\(=(n-i+1)+\displaystyle\sum_{k=1}^{n-i}(-k+n-i+1)\)
\(=(n-i+1)-\displaystyle\sum_{k=1}^{n-i}k+(n-i+1)\displaystyle\sum_{k=1}^{n-i}1\)
\(=(n-i+1)-\displaystyle\frac{1}{2}(n-i)(n-i+1)+(n-i+1)(n-i)\)
\(=\displaystyle\frac{1}{2}(n-i+1)\{2-(n-i)+2(n-i)\}\)
\(=\displaystyle\frac{1}{2}(n-i+1)(n-i+2)\) (\(0≦i≦n\))
(補足)
問題文で、\(i\)の範囲つまり\(x\)の範囲は \(0≦i≦n\) と与えられていますがこれを自力で求めるには、(ア)不等式から考えるか、(イ)平面図で領域がある場合を考えるか、(ウ)空間図で考えるかになります。
(ア)\(x+y+z≦n\) より、\(0≦x≦n\) のときは\(y,z\)が\(0\)以上の値としてとれますが、\(x>n\) のときは\(y,z\)の一方が負になるので不適です。
(イ)\(0≦i≦n\) のときは、切り口において
\(y≧0\), \(z≧0\), \(z≦-y+n-i\)・・・①
で表される領域が存在し格子点も存在しますが(図で書ける)、\(i>n\) のときは、境界線 \(z=-y+n-i\) の\(z\)切片が負になるので①で表される領域が存在しません(格子点がない)。
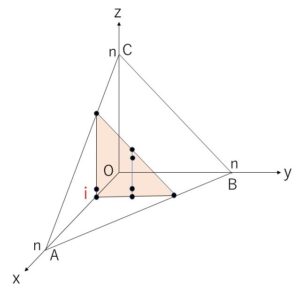
(ウ)\(x+y+z=n\) は空間では平面を表し、\(A(n,0,0),B(0,n,0),C(0,0,n)\) を通ります。
不等式を \(z≦-x-y+n\) と変形すると、この平面の下側が不等式の表す領域で、\(x≧0\), \(y≧0\), \(z≧0\) と合わせると、四面体\(OABC\) の表面および内部が領域\(D\)です。すると切断面は三角形になることや、切り口が存在する(格子点が存在する)のは \(0≦x≦n\) であることなどが分かります。
(2)
(1)より求める格子点の個数は
\(\displaystyle\sum_{i=0}^{n}\displaystyle\frac{1}{2}(n-i+1)(n-i+2)\)
\(=\displaystyle\frac{1}{2}(n+1)(n+2)+\displaystyle\sum_{i=1}^{n}\displaystyle\frac{1}{2}(n-i+1)(n-i+2)\)
\(=\displaystyle\frac{1}{2}(n+1)(n+2)+\displaystyle\frac{1}{2}\displaystyle\sum_{i=1}^{n}i^2-\displaystyle\frac{1}{2}(2n+3)\displaystyle\sum_{i=1}^{n}i+\displaystyle\frac{1}{2}(n+1)(n+2)\displaystyle\sum_{i=1}^{n}1\)
\(=\displaystyle\frac{1}{2}(n+1)(n+2)+\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{6}n(n+1)(2n+1)-\displaystyle\frac{1}{2}(2n+3)\displaystyle\frac{1}{2}n(n+1)+\displaystyle\frac{1}{2}(n+1)(n+2)n\)
\(=\displaystyle\frac{1}{12}(n+1)\{6(n+2)+n(2n+1)-3n(2n+3)+6n(n+2)\}\)
\(=\displaystyle\frac{1}{12}(n+1)(2n^2+10n+12)\)
\(=\displaystyle\frac{1}{6}(n+1)(n^2+5n+6)\)
\(=\displaystyle\frac{1}{6}(n+1)(n+2)(n+3)\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→組合せと数列 back→群数列②