漸化式と不等式に関する例題です。
応用も効く内容です。
(例題)
\(a\)を正の定数とする。\(f(x)=x^2-a\) として、関数\(y=f(x)\)のグラフ上の点\((x_n,f(x_n))\)における接線が\(x\)軸と交わる点の\(x\)座標を\(x_{n+1}\)とする。このようにして、\(x_{1}\)から順に\(x_2,x_3,x_4,\cdots\)を作る。ただし、\(x_1>\sqrt{a}\)とする。
(1)\(x_{n+1}\)を\(x_n\)を用いて表せ。
(2)\(\sqrt{a}<x_{n+1}<x_n\) であることを示せ。
(3)\(|x_{n+1}-\sqrt{a}|<\displaystyle\frac{1}{2}|x_{n}-\sqrt{a}|\) であることを示せ。
(4)\(|x_n-\sqrt{a}|<\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|\) であることを示せ。
(解答)
(1)
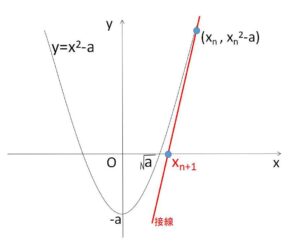
\(y=f(x)=x^2-a\)
\((x_n,x_n^2-a)\) における接線の方程式は、\(f'(x)=2x\) より
\(y=2x_n(x-x_n)+x_n^2-a\)
この接線の\(x\)切片が\(x_{n+1}\)だから
\(0=2x_n(x_{n+1}-x_n)+x_n^2-a\)
よって
\(2x_nx_{n+1}=x_n^2+a\)・・・①
ここで、\(x_n=0\) とすると ①は \(0=a\) となるが、\(a\)は正の定数となるから不適。
ゆえに\(x_n≠0\)だから①の両辺を\(2x_n\)で割って
\(x_{n+1}=\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n}\)
(2)
不等式の証明の基本は、各辺の差をとることですが、\(\sqrt{a}<x_n\) のほうは\(n\)が自然数であることと、漸化式が手に入っていることから帰納法で示していきます。
(ア)まず \(\sqrt{a}<x_{n}\) を数学的帰納法により示す。
(i)\(n=1\) のとき
条件から \(x_1>\sqrt{a}\) だから成立
(ii)\(n=k\) のとき (\(k=1,2,\cdots\))
\(\sqrt{a}<x_{k}\) が成り立つと仮定する。
このとき漸化式より
\(x_{k+1}-\sqrt{a}\)
\(=\displaystyle\frac{1}{2}x_k+\displaystyle\frac{a}{2x_k}-\sqrt{a}\)
\(=\displaystyle\frac{x_k^2+a-2\sqrt{a}x_k}{2x_{k}}\)
\(=\displaystyle\frac{(x_k-\sqrt{a})^2}{2x_{k}}>0\)
したがって \(\sqrt{a}<x_{k+1}\) であり、\(n=k+1\)でも成立する。
(i)(ii)より、任意の自然数\(n\)で \(\sqrt{a}<x_n\)
(イ)次に、\(x_{n+1}<x_n\) を示す。
\(x_{n}-x_{n+1}\)
\(=x_{n}-(\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n})\)
\(=\displaystyle\frac{x_n^2-a}{2x_{n}}>0\) (∵(ア)より \(x_n^2>a\) )
よって \(x_{n+1}<x_n\)
(ア)(イ)より
\(\sqrt{a}<x_{n+1}<x_n\)
(3)
なおこの例題だと絶対値はあっても無くても変わりませんが、正負どちらにも対応できるように絶対値をつけることが多いです。詳しくは解答後の(参考)を見て下さい。
\(|x_{n+1}-\sqrt{a}|\)
\(=|\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n}-\sqrt{a}|\)
\(=\left|\displaystyle\frac{(x_n-\sqrt{a})^2}{2x_{n}}\right|\)
\(=\left|\displaystyle\frac{x_n-\sqrt{a}}{2x_n}\right||x_n-\sqrt{a}|\)
\(=\displaystyle\frac{1}{2}\left|(1-\displaystyle\frac{\sqrt{a}}{x_n})\right||x_n-\sqrt{a}|\)
ここで(2)より \(x_n>\sqrt{a}\ (>0)\) だから
\(0<\displaystyle\frac{\sqrt{a}}{x_n}<1\)
よって
\(\left|(1-\displaystyle\frac{\sqrt{a}}{x_n})\right|<1\)
となるから
\(|x_{n+1}-\sqrt{a}|<\displaystyle\frac{1}{2}|x_n-\sqrt{a}|\)
(4)
\(a_n=2a_{n-1}=2^2a_{n-2}=2^3a_{n-3}=\cdots=2^{n-1}a_1\)
となります。これと同じことを不等式でもやります。(3)の不等式は両辺で1つずれた形になっているのでこの方法が使えます。
(3)より
\(|x_{n}-\sqrt{a}|<\displaystyle\frac{1}{2}|x_{n-1}-\sqrt{a}|\)
\(<\displaystyle\frac{1}{2^{2}}|x_{n-2}-\sqrt{a}|\)
\(<\displaystyle\frac{1}{2^{3}}|x_{n-3}-\sqrt{a}|\)
\(\cdots<\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|\)
よって
\(|x_n-\sqrt{a}|<\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|\)
(参考)極限と近似値
(4)で証明した不等式
\(|x_n-\sqrt{a}|<\displaystyle\frac{1}{2^{n-1}}|x_1-\sqrt{a}|\)
より、\(n\)をどんどん大きくしていくと右辺はどんどん小さくなっていき、\(0\)に近づいていく。よってこの不等式から\(n\)を大きくしていくと、\(x_n\)は\(\sqrt{a}\)に近づくことが分かる。実際、極限(数Ⅲ)を求めると
\(\displaystyle\lim_{n \to \infty}x_n=\sqrt{a}\)
となる。また、(2)で証明した不等式
\(x_{n+1}<x_{n}\) (ただし \(x_1>\sqrt{a}\))
より、この数列は単調減少となるから、\(n\)が大きいほど\(x_n\)は\(\sqrt{a}\)に近い。
((3)の不等式からも分かる)
またこの数列の漸化式は
\(x_{n+1}=\displaystyle\frac{1}{2}x_n+\displaystyle\frac{a}{2x_n}\)
であるから、\(a\)が有理数のとき、条件 \(x_1>\sqrt{a}\) を満たすような有理数\(x_1\)を選べば、漸化式に次々に代入することによって、有理数 \(x_2,x_3,x_4,\cdots\) が求まり、項を増やすことでより\(\sqrt{a}\)により近い数を求めることができる。(有理数なので 分子÷分母 で値が計算できる)
このようにして\(\sqrt{a}\)の近似値を高い精度で求めることができる。(ニュートン法とよばれる)
なお、\(x_n-\sqrt{a}\) のような差がいつも正の値とは限らないので、極限や近似値を求める際には絶対値を付けることが多い。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
back→漸化式と互いに素(逆向き帰納法)