平面や空間の分割に関する例題です。
(例題1)
平面上に\(n\)本の直線があって、どの2本も平行でなく、またどの3本も1点で交わらないとする。これら\(n\)本の直線が平面を\(a_n\)個の領域に分けるとするとき、\(a_n\)を\(n\)の式で表せ。
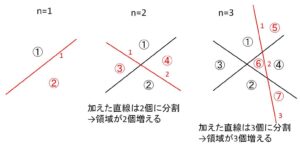
(解答)
\(n\)本の直線により\(a_{n}\)個の領域に分けられているときに、\(n+1\)本目の直線を加えると、加えた直線は既にある\(n\)本の直線と\(n\)個の異なる点で交わり、加えた直線は\(n+1\)個の部分に分割される。そしてこの分割された個数の分だけ領域が増えるので
\(a_{n+1}=a_n+(n+1)\) (階差型)
また \(a_1=2\) だから\(n≧2\)のとき
\(a_{n}=a_1+\displaystyle\sum_{k=1}^{n-1}(k+1)\)
\(=2+\displaystyle\frac{1}{2}(n-1)n+(n-1)\)
\(=\displaystyle\frac{1}{2}n^2+\displaystyle\frac{1}{2}n+1\) (\(n=1\)でも成立)
(例題2)
平面上にどの2つをとっても互いに2点で交わり、またどの3つをとっても同一の点で交わらない\(n\)個の円がある。これらの円が平面を\(a_n\)個の領域に分けるとするとき、\(a_n\)を\(n\)の式で表せ。
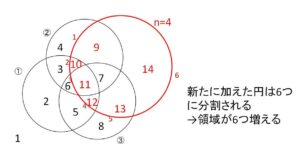
(解答)
\(n\)個の円で平面が\(a_n\)個の領域に分けられているとき、\(n+1\)個目の円を条件にあうように加えると、既にあった\(n\)個の円とそれぞれ2点ずつ交わりこれらの交点はすべて異なるので、新たに加えた円は\(2n\)個の弧に分割される。そして分割された部分の個数の分だけ領域が増えるので
\(a_{n+1}=a_n+2n\) (階差型)
また、\(a_1=2\) だから \(n≧2\) のとき
\(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}2k\)
\(=2+\displaystyle\frac{2}{2}(n-1)n\)
\(=n^2-n+2\) (\(n=1\)でも成立)
(例題3)
空間に相違なる平面\(α_0,α_1,\cdots,α_n,\cdots\)があり、次の条件をみたしている。
(i)どの2平面も平行でない。
(ii)2枚の平面の交線は、どの2本も平行でない。
(iii)どの3平面も同一直線を共有しない。
(iv)どの4平面も1点では交わらない。
(1)平面\(α_0\)と平面\(α_k\) (\(k≧1\)) とが交わってできる直線を\(l_k\)で表す。平面\(α_0\)が直線\(l_1,l_2,\cdots,l_n\)によって分割された部分の個数\(f(n)\)を求めよ。
(2)空間が平面\(α_1,α_2,\cdots,α_n\)によって分割された部分の個数\(F(n)\)を求めよ。
(解答)
(1)
\(n\)枚の平面\(α_1~α_n\)に\(α_0\)を加えると、(i)~(iv)の条件からその交わりは\(n\)本の直線になり、どの2本も平行でなく、どの3本も1点で交わらない配置になります。(i)~(iv)の条件がないと、これらの直線の本数が減ったり、平行になったり、3本以上の直線が1点で交わったりします(詳しくは後で説明します)。
よって、(1)は平面の直線による分割で、(例題1)と同じです。
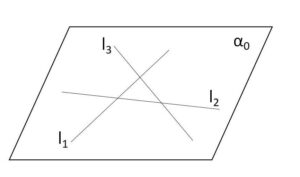
平面\(α_0\)と平面\(α_1~α_n\)との交わりは異なる\(n\)本の直線であり、これらの直線は「どの2本も平行でなく、どの3本も1点で交わらない。」・・・①
平面\(α_0\)が\(n\)本の直線\(l_1,l_2,\cdots,l_n\)により\(f(n)\)個の領域に分けられているとき、\(n+1\)本目の直線を①を満たすように加えると、\(n+1\)個の領域が増えるので
\(f(n+1)=f(n)+(n+1)\)
を満たす。\(f(1)=2\) だから、\(n≧2\)のとき
\(f(n)=f(1)+\displaystyle\sum_{k=1}^{n-1}(k+1)\)
\(=2+\displaystyle\frac{1}{2}(n-1)n+(n-1)\)
\(=\displaystyle\frac{1}{2}n^2+\displaystyle\frac{1}{2}n+1\)
(\(n=1\)でも成立)
(注)条件(i)~(iv)について
(i)どの2平面も平行でない。
平行だと交わりが無いので、交線が減ります。
(ii)2枚の平面の交線は、どの2本も平行でない。
例えば\(n=3\)のとき、\(α_1,α_2\)の交線に平行に3枚目の平面\(α_3\)を入れると、\(α_3\)上では\(α_1,α_2\)は交わらないので、\(α_3\)上において\(α_1,α_2\)との交線(2直線)は、平行になる。
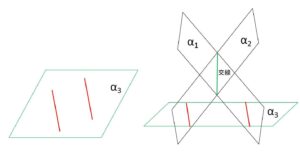
また(i)(ii)を合わせて「どの3平面も少なくとも1点で交わる」とする場合もあります。
(iii)どの3平面も同一直線を共有しない。
例えば\(n=3\)のとき、\(α_1,α_2\)の交線すべてを含むように平面\(α_3\)を入れると、\(α_3\)上で\(α_1,α_2\)との交線は1本になる。
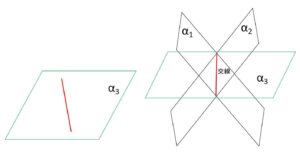
(iv)どの4平面も1点では交わらない。
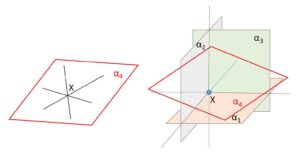
例えば\(n=4\)のとき、\(α_1,α_2,α_3\)の交わり(1点\(X\))を通るように\(α_4\)を入れると、\(α_4\)上で\(α_1,α_2,α_3\)との交線(3直線)はどれも交点\(X\)を通ることから、3直線が\(α_4\)上で1点\(X\)で交わることになる。
(2)
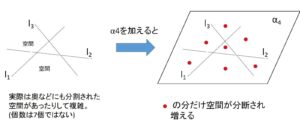
\(n\)個の平面\(α_1~α_n\)によって空間が\(F(n)\)個に分割されているとき、\(n+1\)個目の平面\(α_{n+1}\)を追加すると、既にある\(n\)個の平面によって追加した平面\(α_{n+1}\)は(1)の\(f(n)\)個に分割される。分割された個数の分だけ領域(空間)が増えるので
\(F(n+1)=F(n)+\displaystyle\frac{1}{2}n^2+\displaystyle\frac{1}{2}n+1\) (階差型)
\(F(1)=2\) より \(n≧2\) のとき
\(F(n)=F(1)+\displaystyle\sum_{k=1}^{n-1}(\displaystyle\frac{1}{2}k^2+\displaystyle\frac{1}{2}k+1)\)
\(=2+\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{6}(n-1)n(2n-1)+\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{2}(n-1)n+(n-1)\)
\(=\displaystyle\frac{1}{6}n^3+\displaystyle\frac{5}{6}n+1\)
(\(n=1\)でも成立)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→確率・場合の数と漸化式① back→図形と数列・漸化式①