問題文で漸化式の記述がない確率・場合の数の問題で、漸化式を使う例題について見ていきます。
(1)直接計算する (2)漸化式を立てる
どちらの方法を選ぶかの目安は、
(1) \(n=1,2\)などの具体例を簡単に一般化できる場合
(2) (1)のように単純に一般化はできないが、\(n\)と\(n+1\)の関連が分かる場合
です(どちらの方法でも解ける場合もあります)。解法の手段として(1)(2)を頭に入れつつ、(1)で無理なら(2)でやるのような取り組み方をするとよいと思います。漸化式の記述がない場合で自力で漸化式を立てるのは少しハードルが高いかもしれませんが、方程式を立てて未知数を求めるくらいの感覚で漸化式を立てるようにするとよいと思います。
今回は漸化式を立てる(2)の方針で解く例題を扱って、次回に(1)の方針で特にシグマ計算を利用する例題について扱います。
(例題1)
2つの箱\(A,B\)のそれぞれに赤玉が\(1\)個、白玉が\(3\)個、合計\(4\)個ずつ入っている。\(1\)回の試行で箱\(A\)の玉\(1\)個と箱\(B\)の玉\(1\)個を無作為に選び交換する。この試行を\(n\)回繰り返した後、箱\(A\)に赤玉が\(1\)個、白玉が\(3\)個入っている確率\(p_n\)を求めよ。
(解答)
(i)赤\(0\) 白\(4\) (ii)赤\(1\) 白\(3\) (iii)赤\(2\) 白\(2\)
の3パターンです。(ii)の状態が求める確率の状態で、\(n\)回の操作で(i)(ii)(iii)のいずれかになっています。\(n+1\)回目で(ii)の状態にするには (i)→(ii)、 (ii)→(ii)、(iii)→(ii) の分岐になりますが、(i)→(ii) と (iii)→(ii) は同じ確率になることに気づくと未知の数列が\(p_n\)1つで済みます。
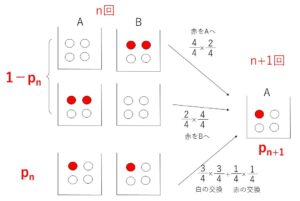
\(n\)回の操作後の箱\(A\)の状態は
(赤玉の個数,白玉の個数)\(=(0,4),(1,3),(2,2)\)
のいずれかである。これらの状態から\(n+1\)回目の操作後に (赤玉の個数,白玉の個数)\(=(1,3)\) になるときを考えると
(ア)\(n\)回で (赤玉の個数,白玉の個数)\(=(0,4),(2,2)\) のとき
いずれも確率は、\(\displaystyle\frac{4}{4}\cdot\displaystyle\frac{2}{4}=\displaystyle\frac{1}{2}\)
(イ)\(n\)回で (赤玉の個数,白玉の個数)\(=(1,3)\) のとき
同色の玉を交換すればよいので確率は
\(\displaystyle\frac{3}{4}\cdot\displaystyle\frac{3}{4}+\displaystyle\frac{1}{4}\cdot\displaystyle\frac{1}{4}=\displaystyle\frac{5}{8}\)
よって\(p_{n+1}\)と\(p_n\)について次の関係式が成り立つ。
\(p_{n+1}=(1-p_n)\cdot\displaystyle\frac{1}{2}+p_n\cdot\displaystyle\frac{5}{8}\)
整理して
\(p_{n+1}=\displaystyle\frac{1}{8}p_n+\displaystyle\frac{1}{2}\)
また
\(p_1=\displaystyle\frac{3}{4}\cdot\displaystyle\frac{3}{4}+\displaystyle\frac{1}{4}\cdot\displaystyle\frac{1}{4}=\displaystyle\frac{5}{8}\)
漸化式の特性方程式
\(x=\displaystyle\frac{1}{8}x+\displaystyle\frac{1}{2}\)
を解くと \(x=\displaystyle\frac{4}{7}\) だから、漸化式は次のように変形できる。
\(p_{n+1}-\displaystyle\frac{4}{7}=\displaystyle\frac{1}{8}(p_n-\displaystyle\frac{4}{7})\)
ゆえに
\(p_n-\displaystyle\frac{4}{7}=(p_1-\displaystyle\frac{4}{7})(\displaystyle\frac{1}{8})^{n-1}=\displaystyle\frac{3}{7\cdot8}(\displaystyle\frac{1}{8})^{n-1}\)
したがって
\(p_n=\displaystyle\frac{3}{7}(\displaystyle\frac{1}{8})^{n}+\displaystyle\frac{4}{7}\)
(例題2)
先頭車両から順に\(1\)から\(n\)までの番号のついた\(n\)両編成の列車がある。ただし、\(n≧2\) とする。各車両を赤色、青色、黄色のいずれか\(1\)色で塗るとき、隣り合った車両の少なくとも一方が赤色となるような色の塗り方は何通りか。
(1)1両目の色で場合分け (2)\(n\)両目と\(n+1\)両目の関連を考える
方法があります。(1)のほうが計算は楽です。
(解答1)1両目で場合分け
(i)赤色で塗ると、2両目は何色でもいいので2両目以降残りの\(n\)両の塗り方は\(a_n\)通り。
(ii)青色で塗ると、2両目は赤色で塗るしかないです。そして3両目は何色でもいいので3両目以降残りの\(n-1\)両の塗り方は\(a_{n-1}\)通りです。黄色でも同様です。
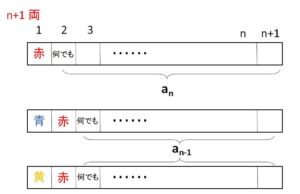
\(n\)両列車の塗り方を\(a_n\)する。\(n+1\)両列車の塗り方は
(i)1両目を赤色で塗るとき、2両目は何色で塗ってもよいので\(a_n\)通り。
(ii)1両目を青色または黄色で塗るとき、2両目は赤色で塗ることになり、3両目は何色でもよいのでそれぞれ\(a_{n-1}\)ずつ。
したがって次の漸化式が成り立つ。
\(a_{n+1}=a_n+2a_{n-1}\)
\(a_n\) を \(n=1\) から定義しても漸化式は成り立ち
\(a_1=3\) (3色で3通り)
\(a_2\)については、(1両目,2両目)=(赤,赤), (赤,青), (赤,黄), (青,赤), (黄,赤) の場合があるから
\(a_2=5\)
漸化式の特性方程式
\(x^2=x+2\) を解くと \(x=-1,2\) だから漸化式は次のように変形できる。
\(a_{n+1}+a_{n}=2(a_n+a_{n-1})\)
\(a_{n+1}-2a_n=-(a_n-2a_{n-1})\)
よって
\(a_{n+1}+a_{n}=(a_2+a_1)\cdot2^{n-1}=8\cdot2^{n-1}=2^{n+2}\)・・・①
\(a_{n+1}-2a_n=(a_2-2a_1)(-1)^{n-1}=(-1)\cdot(-1)^{n-1}=(-1)^n\)・・・②
(①-②)÷3 より
\(a_n=\displaystyle\frac{1}{3}\{2^{n+2}-(-1)^{n}\}\)
したがって
\(\displaystyle\frac{1}{3}\{2^{n+2}-(-1)^{n}\}\) 通り
(解答2)\(n\)両目と\(n+1\)両目の関連
(ア)赤色のとき、\(n+1\)両目は3色どれでもよい
(イ)青色 or 黄色 のとき、\(n+1\)両目は赤色のみ
のパターンになります。この方法だと\(n\)両目の塗り方で場合分けしているので、複数の数列を未知のものとしておく必要があります(連立漸化式になる)。
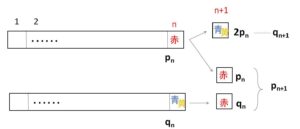
\(n\)両の列車において、\(n\)両目が赤色で塗られているときの塗り方の総数を\(p_n\)、\(n\)両目が赤色以外(青色または黄色)で塗られているときの塗り方の総数を\(q_n\)とおく。求める塗り方の総数は\(p_n+q_n\)である。
(未知の数列が2個なので2個漸化式を立てます)
\(n+1\)両の列車において
(1)\(n+1\)両目が赤色のときは、\(n\)両目は何色でもよいので次の漸化式が成り立つ。
\(p_{n+1}=p_n+q_n\)・・・(1)
(2)\(n+1\)両目が赤色以外(青色または黄色)のときは、\(n\)両目は赤色だから次の漸化式が成り立つ。
\(q_{n+1}=2p_n\)・・・(2)
(1)より \(p_{n+2}=p_{n+1}+q_{n+1}\)
これに(2)を代入して
\(p_{n+2}=p_{n+1}+2p_n\)・・・(3)
((解答1)と同様に\(p_1\)も定義します)
ここで、\(p_n,q_n\) を \(n=1\) から定義しても漸化式(1)(2)は成り立つので、(3)は\(n=1,2,3,\cdots\) で成り立つとしてよい。
すると
\(p_1=1\) であり、
\(p_2\) については (1両目,2両目)=(赤,赤), (青,赤), (黄,赤) の場合があるので
\(p_2=3\)
(3)の特性方程式は
\(x^2=x+2\) だからこれを解くと \(x=-1,2\)
よって(3)は次のように変形できる。
\(p_{n+2}+p_{n+1}=2(p_{n+1}+p_{n})\)
\(p_{n+2}-2p_{n+1}=-(p_{n+1}-2p_{n})\)
よって
\(p_{n+1}+p_{n}=(p_2+p_1)2^{n-1}=2^{n+1}\)・・・(4)
\(p_{n+1}-2p_{n}=(p_2-2p_1)(-1)^{n-1}=(-1)^{n-1}\)・・・(5)
{(4)-(5)}÷3 より
\(p_n=\displaystyle\frac{1}{3}\{2^{n+1}+(-1)^{n}\}\)
よって(2)より
\(q_n\)\(=2p_{n-1}\)\(=\displaystyle\frac{2}{3}\{2^{n}+(-1)^{n-1}\}\) (\(n≧2\))
(\(n=1\)でも成り立ちますが、問題設定は\(n≧2\)なのでこのままにしておきます)
したがって求める塗り方の総数は
\(p_n+q_n\)
\(=\displaystyle\frac{1}{3}\{2^{n+1}+(-1)^{n}\}+\displaystyle\frac{2}{3}\{2^{n}+(-1)^{n-1}\}\)
\(=\displaystyle\frac{1}{3}\{2\cdot2^{n}+(-1)^{n}\}+\displaystyle\frac{2}{3}\{2^{n}-(-1)^{n}\}\)
\(=\displaystyle\frac{1}{3}\{2^{n+2}-(-1)^{n}\}\) (通り)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→確率・場合の数とシグマ計算 back→確率・場合の数と漸化式②