事象の独立と乗法定理①

事象の独立について見ていきます。

 

・事象の独立
サイコロとコインを投げるという試行において、次の2つの事象

事象\(A\):サイコロで\(5\)の目が出る
事象\(B\):コインの表が出る

は互いに影響を与えません。
一般に2つの事象\(A,B\)において、条件付き確率について

\(P_A(B)=P(B)\) または \(P_B(A)=P(A)\)

が成り立つとき、一方の事象の起こることが他方の事象に影響を与えないので、このとき事象\(A\)と事象\(B\)は互いに独立であるといいます(定義)。また事象\(A,B\)が独立でないとき、事象\(A,B\)は互いに従属であるといいます。

ここで確率の乗法定理
\(P(A \cap B)=P(A)P_A(B)\)　(\(P(A \cap B)=P(B)P_B(A)\))
を用いると、事象\(A,B\)が独立のとき次の等式が成り立つことになります。

\(P(A \cap B)=P(A)P(B)\)　(独立な事象における乗法定理)
(それぞれの確率を単に考えて積をとるだけ)

またこれらは同値の関係なので(以下の証明参照)、どれか1つでも成り立てば独立であることが言えます。

(証明)
\(P_A(B)=P(B)\)・・・①
が成り立つとき、乗法定理より
\(P(A \cap B)=P(A)P_A(B)\)・・・②
だから
\(P(A \cap B)=P(A)P(B)\)・・・③
逆に③が成り立つとき、②と③の右辺を比べて
\(P_A(B)=P(B)\)・・・①
となるので
\(P_A(B)=P(B) ⇔ P(A \cap B)=P(A)P(B)\)

同様に
\(P_B(A)=P(A) ⇔ P(A \cap B)=P(A)P(B)\)
が成り立つので

\(P_A(B)=P(B)\)
\(⇔\)\(P_B(A)=P(A)\)
\(⇔\)\(P(A \cap B)=P(A)P(B)\)

の同値関係が分かる。あとは独立の定義によりこれらが独立の必要十分条件となる。

(注)
定義で2つの等式
\(P_A(B)=P(B)\) または \(P_B(A)=P(A)\)
を書きましたが、上記証明から分かるように片方のみでもよいことになります。また同値関係により
\(P(A \cap B)=P(A)P(B)\)
を定義にしてもよいことになります。

 

(参考)
さらに議論を進めると余事象の独立についての同値関係も分かります。つまり

\(A,B\)が独立
\(⇔\)\(\overline{A},B\)が独立
\(⇔\)\(A,\overline{B}\)が独立
\(⇔\)\(\overline{A},\overline{B}\)が独立

です。

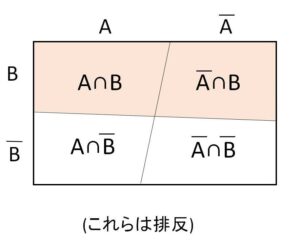
例えば
\(A,B\)が独立 \(⇔\)\(\overline{A},B\)が独立
については
\(P(B)=P(A \cap B)+P(\overline{A} \cap B)\)　(排反事象。上図より)
だから
\(P(\overline{A} \cap B)=P(B)-P(A \cap B)\)・・・(i)

\(A,B\)が独立ならば(i)より
\(P(\overline{A} \cap B)=P(B)-P(A)P(B)\)・・・(ii)
\(P(\overline{A} \cap B)=\{1-P(A)\}P(B)\)
\(P(\overline{A} \cap B)=P(\overline{A})P(B)\)・・・(iii)
よって、\(\overline{A},B\)が独立となる。

逆に\(\overline{A},B\)が独立ならば(iii)つまり(ii)が成り立ち、(i)も合わせると
\(P(A \cap B)=P(A)P(B)\)
が成り立つので、\(A,B\)が独立となる。

(他も同様です)

 

 

・試行の独立
ついでなので試行の独立についても扱っておきます。
「2つの試行が互いに他方の結果に影響を及ぼさない」
とき、この2つの試行は互いに独立であるといいます。

例えば

試行\(S\):サイコロを投げる
試行\(T\):コインを投げる

は独立な試行の代表例です。これらが互いに影響を及ぼさない試行であることは何となく分かると思いますが、丁寧に考えるなら試行\(S,T\)のどの結果も互いに影響を及ぼさない、つまり\(S,T\)から起きる全ての事象が互いに独立であるということです。事象をサイコロの目、コインの表裏に限定することにすると

\(S\)の事象:{1,2,3,4,5,6}
\(T\)の事象:{表,裏}

であり、１回づつ投げるとき「サイコロで5の目 かつ コインで表」が出る確率\(P\)は全事象により考えると
\(P=\displaystyle\frac{1×1}{6×2}\)
であり
\(P=\displaystyle\frac{1}{6}×\displaystyle\frac{1}{2}\)
となり、独立な事象の乗法定理が成り立つので、2つの事象「5の目、表」が独立であることが分かります。他の組み合わせの事象であっても同様なので試行\(S,T\)が独立であることが言えます。本来なら独立な試行をこのように考えるべきかもしれませんが、サイコロとコインのような明らかな例の場合(確率を計算する時の分母分子が単純な積(直積)になっているだけの場合)は、独立な試行であると判断してもよいです。

 

 

 

(例題)
ジョーカーを除いた1組のトランプ\(52\)枚がある。(数字1~13までのスペード、ハート、クローバー、ダイヤのカード計\(52\)枚)
トランプをよくきってから、\(1\)枚のカードを引く。この試行において、ハートを引く事象を\(A\)、エース(数字1)を引く事象を\(B\)、ハートの絵札(数字11~13)を引く事象を\(C\)とするとき、次の事象の独立・従属を調べよ。

(1)事象\(A,B\)
(2)事象\(A,C\)

 

(解答)
(1)
\(P(A)=\displaystyle\frac{13}{52}=\displaystyle\frac{1}{4}\)
\(P(B)=\displaystyle\frac{4}{52}=\displaystyle\frac{1}{13}\)
\(P(A \cap B)=\displaystyle\frac{1}{52}\)　(ハートかつエースを引く)

よって
\(P(A \cap B)=P(A)P(B)\)
が成り立つので、独立。

(2)
\(P(A)=\displaystyle\frac{1}{4}\)
\(P(C)=\displaystyle\frac{3}{52}\)
\(P(A \cap C)=\displaystyle\frac{3}{52}\)　(ハートかつハートの絵札を引く)

よって
\(P(A \cap C)≠P(A)P(C)\)
だから、従属。

 

 

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→事象の独立と乗法定理②(3つ以上の事象)