確率変数の導入について見ていきます。
・確率変数と確率分布

サイコロを1回投げるという試行において、その目に関する事象は \(1,2,3,4,5,6\) のいずれかになり、確率はそれぞれ\(\displaystyle\frac{1}{6}\)です。これを表にすると上図のようになります。
ここで、変数\(X\)を導入してサイコロの出る目を\(X\)とすれば、\(X\)は試行の結果\(1,2,3,4,5,6\)のいずれかの値をとり、それぞれの値に対して確率が定まります。このような変数\(X\)を確率変数といい、通常は大文字の文字を用います。
確率変数を導入するのは、例えば未知の集団の分布などを調べる際に変数を用いたほうがそのグラフの形状(分布の仕方)などを調べるのに都合がいいからです。
サイコロの目や、袋から取り出した赤球の数のようにもともと数値で表されるものはそのまま確率変数として扱えますが、コインの裏表のような試行の結果の場合には確率変数として扱うには、「表は\(1\)、裏は\(0\)」のように対応する値を定めればよいです。
また、確率変数\(X\)に対して具体的な試行の結果、つまり\(X\)が具体的にとる値\(1,2,3,4,5,6\)を実現値や観測値とよび、こちらは小文字の文字を用いて\(x_1,x_2,x_3,x_4,x_5,x_6\)のように表します。
そして、確率変数\(X\)の実現値が\(x_1,x_2,\cdots,x_n\)であるとき、\(X\)がこのうち1つの値\(x_k\)をとる確率を \(P(X=x_k)\) と表し、複数の値をとる場合、例えば\(X\)が\(a\)以上である確率は \(P(X≧a)\) のように表します。
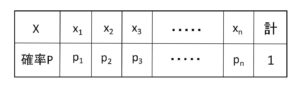
ここで、\(P(X=x_k)=p_k\) と書くことにすると、実現値\(x_1,x_2,\cdots,x_n\)と確率\(p_k\)の対応関係は上図のようになり、この対応関係を\(X\)の確率分布または分布とよび、確率変数\(X\)はこの分布に従うといいます。このとき確率の性質により
\(p_k≧0\) (\(k=1,2,\cdots,n\))
\(p_1+p_2+\cdots+p_n=1\)
が成り立ちます。
なお確率分布の表現方法は上のような表を用いる他に、文字\(k\)を使った数式表現などもあります(さらに確率を縦軸、\(k\)を横軸とすればグラフも書ける)。
(例題)
\(n\)を\(2\)以上の整数とする。\(1\)から\(2n\)までの整数から無作為に相異なる\(3\)つの数を取り出して、それらの最大の数と最小の数の差を\(X\)とする。
(1)確率変数\(X\)の確率分布を求めよ。
(2)\(X\)の値が\(n\)以下となる確率を求めよ。
(解答)
(1)
\(3\)つの数の選び方は、\({}_{2n}\mathrm{C}_3\)通り。
\(X\)のとりうる値は \(2≦X≦2n-1\) であるので、
\(X=k\) (\(2≦k≦2n-1\))
とおいたとき、\(X=k\) となる3数の組み合わせは小さい順に
\(\{a,b,a+k\}\)
とおける。
\(a\)を1つ決めると、3つのうち最も大きい数は\(a+k\)と定まり、また \(a+k≦2n\) だから\(a\)のとりうる範囲は
\(1≦a≦2n-k\)・・・①
\(b\)のとりうる範囲は
\(a+1≦b≦a+k-1\)・・・②
よって①の\(2n-k\)通りの\(a\)の値に対して、②より各々\(b\)は
\((a+k-1)-(a+1)+1=k-1\)
通りの場合があるので、\(X\)の確率分布は次のように表される。
\(P(X=k)=\displaystyle\frac{(2n-k)(k-1)}{{}_{2n}\mathrm{C}_3}\)
\(=\displaystyle\frac{3!(2n-k)(k-1)}{2n(2n-1)(2n-2)}\)
\(=\displaystyle\frac{3(2n-k)(k-1)}{2n(2n-1)(n-1)}\) (\(2≦k≦2n-1\))
(2)
求める確率は
\(P(X≦n)=\displaystyle\sum_{k=2}^{n}\displaystyle\frac{3(2n-k)(k-1)}{2n(2n-1)(n-1)}\)
(\(k=1\)のとき確率はちょうど\(0\)になるので含めて計算すると)
\(=\displaystyle\sum_{k=1}^{n}\displaystyle\frac{3(2n-k)(k-1)}{2n(2n-1)(n-1)}\)
\(=\displaystyle\frac{3}{2n(2n-1)(n-1)}\displaystyle\sum_{k=1}^{n}\{-k^2+(2n+1)k-2n\}\)
\(=\displaystyle\frac{3}{2n(2n-1)(n-1)}\left\{-\displaystyle\frac{1}{6}n(n+1)(2n+1)+(2n+1)\cdot\displaystyle\frac{1}{2}n(n+1)-2n^2\right\}\)
\(=\displaystyle\frac{3}{2n(2n-1)(n-1)}\left\{\displaystyle\frac{1}{3}n(2n^2-3n+1)\right\}\)
\(=\displaystyle\frac{3}{2n(2n-1)(n-1)}\cdot\displaystyle\frac{1}{3}n(2n-1)(n-1)\)
\(=\displaystyle\frac{1}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→確率変数の期待値 back→事象の独立と乗法定理②