確率変数の分散・標準偏差について見ていきます。
これも変数を用いないものと同じです。
・確率変数の分散・標準偏差
(i)\(X=1,-1\): \(p=\displaystyle\frac{1}{2},\displaystyle\frac{1}{2}\)
(ii)\(X=0\): \(p=1\)
上記(i)(ii)の期待値はいずれも\(0\)であるため、期待値だけだとこれらの確率分布の違いを表すことができません。そこで分布の散らばりを表す量として分散(\(V(X)\))というものを定義します。確率変数\(X\)の分散は期待値(平均)を\(m\)とおくと、次の式で表されます。
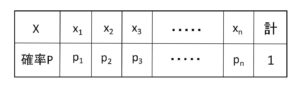
\(V(X)=\displaystyle\sum_{k=1}^{n}(x_k-m)^2p_k\)
\(=(x_1-m)^2p_1+(x_2-m)^2p_2+\cdots+(x_n-m)^2p_n\)
\(V(X)\)の\(V\)は Variance(分散) の頭文字です。分散を単に文字\(σ\)(シグマ)を使って、\(σ^2\)で表すこともあります。
平均(期待値)からの距離の2乗の和をとっているので、平均からどれくらいの広がり(散らばり)があるかを表す量であることが分かります。ただの差 \(x_1-m\) にしてしまうと、平均より大きいものと小さいものが打ち消しあってしまい意味がなくなってしまうので、絶対値 \(|x_1-m|\) をとるか 2乗 \((x_1-m)^2\) をとるかになりますが、2乗のほうが処理がしやすいのでこちらを採用しています。
また\(Y=(X-m)^2\) とおくと、\(V(X)\)は\(Y\)の期待値\(E(Y)\)になっているので、分散を期待値を用いて次のように表現することもできます。
\(V(X)=E(Y)=\)\(E((X-m)^2)\)
さらに、分散を式変形することで次のようにも表すことが可能です。
\(V(X)=(x_1-m)^2p_1+(x_2-m)^2p_2+\cdots+(x_n-m)^2p_n\)
\(=(x_1^2p_1+x_2^2p_2+\cdots+x_n^2p_n)\)
\(-2m(x_1p_1+x_2p_2+\cdots+x_np_n)+m^2(p_1+p_2+\cdots+p_n)\)
\(=\displaystyle\sum_{k=1}^{n}x_k^2p_k-2m\cdot m+m^2\cdot1\)
\(=\displaystyle\sum_{k=1}^{n}x_k^2p_k-m^2\)
\(=E(X^2)-\{E(X)\}^2\)・・・①
①は分散を具体的に計算する時などでよく利用します。
しかし、分散は2乗和をとっているので値が大きくなりやすく、またその単位も\(X\)の単位の2乗になっているので、これらのことを解消するために分散の正の平方根をとった標準偏差(\(σ(X)\))を定義します。つまり確率変数\(X\)の標準偏差は
\(σ(X)=\sqrt{V(X)}\)
です。\(σ(X)\)の\(σ\)は英文字だと\(s\)に対応し、standard deviation (標準偏差)に由来します。標準偏差は単に\(σ\)で表されることもあります。
平方根をとっただけなので、標準偏差も分散と同様に散らばりを表す量です。
(参考)数IAデータの分析との対応関係について
\(n\)個のデータ \(x_1,x_2,\cdots,x_n\) があるとき、その平均値\(\bar{x}\)と分散\(s^2\)は次のように表されました。
\(\bar{x}=\displaystyle\frac{1}{n}(x_1+x_2+\cdots+x_n)\)
\(s^2=\displaystyle\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2\}\)
これらは各データの値が等確率\(\displaystyle\frac{1}{n}\)でとりうるとすれば、確率変数での期待値(平均値)、分散と同じになります。
(例題)
点\(P\)が数直線上を原点から出発して動く。硬貨を投げて表が出れば\(P\)は正の方向に\(2\)だけ動き、裏が出れば負の方向に\(1\)だけ動く。\(4\)回硬貨を投げたときの点\(P\)の座標を確率変数\(X\)とする。\(X\)の分散と標準偏差を求めよ。
分散は定義式(差の2乗を素直に計算)か \(E(X^2)-\{E(X)\}^2\) で求めますが、後者のほうが計算が楽になることが多いです。(分布が期待値付近にあつまっている場合には定義式から求めほうが楽なる)
(解答)
表が出る回数を\(k\)回 (\(0≦k≦4\)) とすると、裏が出る回数は\(4−k\)回。
表が\(k\)回出る確率\(p_k\)は
\(p_k={}_4\mathrm{C}_{k}(\displaystyle\frac{1}{2})^k(\displaystyle\frac{1}{2})^{4−k}={}_4\mathrm{C}_k(\displaystyle\frac{1}{2})^4\)・・・①
表\(k\)回に対応する\(P\)の座標\(X\)は
\(X=2k−(4−k)=3k−4\)・・・②
①②で \(k=0,1,2,3,4\) を代入することで確率分布は次のように得られる。
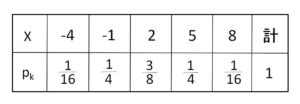
よって期待値は
\(E(X)=(−4)⋅\displaystyle\frac{1}{16}+(−1)⋅\displaystyle\frac{1}{4}+2⋅\displaystyle\frac{3}{8}+5⋅\displaystyle\frac{1}{4}+8⋅\displaystyle\frac{1}{16}\)
\(=2\)
したがって分散は
\(V(X)=E(X^2)-\{E(X)\}^2\)
\(=(−4)^2⋅\displaystyle\frac{1}{16}+(−1)^2⋅\displaystyle\frac{1}{4}+2^2⋅\displaystyle\frac{3}{8}+5^2⋅\displaystyle\frac{1}{4}+8^2⋅\displaystyle\frac{1}{16}-2^2\)
\(=9\)
標準偏差は
\(σ(X)=\sqrt{9}=3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→確率変数の変換(1次式) back→確率変数の期待値