これからこの分野のメインテーマである、統計的な推測についてまずその概要を説明したいと思います。統計的な推測では、一部その証明を省略した定理なども登場し、どうしても暗記に頼らざるを得ない部分が出てきます。また途中で何をやっているかよく意味が分からないということにも陥りやすいです。そこで、意味を持たせた内容のある暗記になるように話を進めていきたいと思います。もちろん大部分は理由付けされた(証明された)内容になっているので、暗記ばかりに頼るのもおススメはしません。
まずは最初の段階として、ざっくりと統計的な推測の流れをつかんでください。既に学習済みの方も内容の整理として見て頂いても構いません。
数学が実生活に応用されていることを肌で感じることできる分野だと思います。意外と内容は面白いですよ。
・統計的な推測の概要
例えばあるお菓子会社が、一世帯当たりどれくらい自社の製品を購入しているか、その平均の購入額(\(1\)ヶ月あたり)を知りたいとします。
調査対象を日本に限定するとして、もちろん日本の全世帯のデータが得られれば、真の平均を知ることができて話は早いです。しかし、それは時間も労力も費用もかかりすぎるので、
「一部の世帯の調査をして、全体の平均を予想する」
という方法をとることになるでしょう。これが統計的な推測の基本的な考えです。
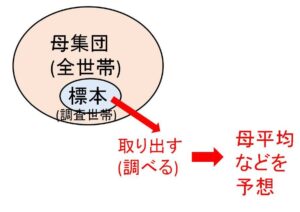
さて最初に設定した調査は、日本の全世帯の中から一部の世帯を選んで調べるということになりますが、例えば調査する世帯数を\(1000\)世帯ということにしましょう。統計ではこの場合の全世帯を母集団、選んだ(取り出した)世帯を標本(サンプルともいう)とよびます。
今知りたいのは一世帯当たりの平均購入額なので、調べた\(1000\)世帯の額の平均(合計して\(1000\)で割ればよい)をとればよさそうです。これを標本平均とよび\(\overline{X}\)のようにバーを使って表します。もちろんこの標本平均が真の平均(母平均)になるとは限りませんし、標本の選び方によって毎回標本平均の値は変わりますが、この標本平均は統計的な推測でものすごく重要な要素になっています。
なぜかというと、調査する世帯数\(n\)が大きいと(今回の\(n=1000\)は大きいとしてよい)、中心極限定理という定理が使えて、母集団がどんな分布をしていても(母集団の分布が分からなくても)、標本平均\(\overline{X}\)が正規分布に従うことから、\(\overline{X}\)を用いて母平均がどの範囲にあるかを予想できるからです。
この分野では平均の他にも比率という内容も扱います。
ある政党の支持率などがその例で、これは\(0\)以上\(1\)以下の割合で表されます。(\(56%\)のような\(%\)表示で表すこともあります)
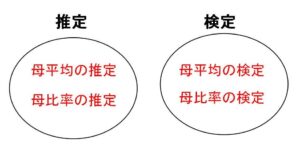
平均でいう母平均と標本平均が、母比率と標本比率になり細かい内容は違いますが、大まかな考え方は平均の場合と同じです。
もちろん検定独自の内容もありますが、推定の内容を多く含んでいるので、まずは推定から理解することが大切です。
(数Bで扱う内容)
以上が統計的な推測の概要ですが、母集団全体を調べることはせずその一部を標本として取り出して議論することになり、得られるデータはその都度変わることがほとんどです。
よって議論やその結論は確率的なものであり、また議論を進めるために確率変数を設定し今まで扱った確率変数に関する定理もフル活用することになります。
全体を一部から予想するために、このような判断になってしまうのです。
あとは細かい内容は単元ごとにその都度おさえるだけです。
それと具体的な演習も重要です。センター試験や共通テストの過去問などがおススメなので解いてみて下さい。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→母集団分布 back→正規分布に関する例題