母比率の二項分布に関連した例題です。
(1)標本比率の分布→母比率の推定
(2)確率\(p\)で特性をもつ標本を抽出→二項分布
のパターンが存在し、今回は(2)のケースの例題を扱います。(本質的には(1)(2)は同じ内容ですが、敢えて別物にして扱うことにします)
例えば、\(p=0.4\) の割合で母集団に特性\(A\)をもつ個体が存在するとき、この中から\(n\)個だけ標本を抽出するとき、各抽出は「特性\(A\)をもつ個体を 引くか(確率\(p\)) 引かないか (確率\(1-p\))」という操作になるので、特性\(A\)をもつ個体の抽出した合計数を\(X\)とすれば、\(X\)は二項分布に従います。もちろん復元抽出とみなしてはいます。
(例題1)
ある市の高校生全員を母集団とし、ある1週間に市立図書館を利用した生徒の割合(母比率)を\(p\)とする。この母集団から\(600\)人を無作為に選んだとき、その1週間に市立図書館を利用した生徒の数を確率変数\(X\)で表す。
(1)まず\(p=0.4\)とする。\(X\)が従う分布を答え、また\(X\)の平均値と標準偏差を求めよ。
(2)標本数\(600\)は十分に大きいので、\(X\)はある分布に近似的に従う。この分布を答えよ。またこの分布の平均値と標準偏差を求めよ。
(3)今度は、\(p=0.2\) とする。\(X\)の平均値と標準偏差は(1)の場合と比べてそれぞれ何倍になるか答えよ。
(1)
\(X\)は二項分布 \(B(600,0.4)\) に従う。
よって
\(E(X)=600\cdot0.4=\)\(240\)
\(σ(X)=\sqrt{600\cdot0.4\cdot0.6}=\)\(12\)
(2)
標本数\(600\)が十分大きいから、\(X\)は正規分布に近似的に従う。この平均値と標準偏差は(1)で求めた値と同じで、それぞれ\(240,12\)
(3)
\(p=0.2\) のとき \(X\)は二項分布 \(B(600,0.2)\) に従う。
このとき
\(E(X)=600\cdot0.2=120\)
\(σ(X)=\sqrt{600\cdot0.2\cdot0.8}=4\sqrt{6}\)
だから
(1)の結果と比べると
期待値: \(\displaystyle\frac{1}{2}\) 倍
標準偏差: \(\displaystyle\frac{\sqrt{6}}{3}\) 倍
(例題2)
有権者が\(1\)万人を超えるある地域で選挙が実施された。
今回実施された選挙の有権者全員を対象として、今回の選挙と前回の選挙のそれぞれについて、投票したか、棄権したか(投票しなかった)かを調査した。今回の選挙については
「今回投票、今回棄権」
の2通りのどちらかであるかを調べ、前回の選挙については、選挙権がなかった者が含まれているので
「前回投票、前回棄権、前回選挙権なし」
の3通りのいずれかであるかを調べた。この調査の結果は下の表のようになった。
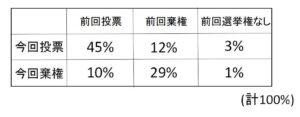
例えば、この有権者全体において、今回棄権かつ前回投票の人の割合は\(10%\)であることを示している。
(1)この有権者全体から無作為に\(1\)人選ぶとき、今回投票の人が選ばれる確率を求めよ。また前回投票の人が選ばれる確率を求めよ。
(2)今回の有権者全体から\(900\)人を無作為に抽出する。その中で、今回棄権かつ前回投票の人数を表す確率変数を\(X\)とする。このとき、\(X\)は二項分布 \(B(n,p)\) に従う。\(n,p\)の値を求めよ。
(3)\(X\)の期待値と標準偏差を求めよ。
(解答)
(1)
表より、今回投票の人が選ばれる確率\(p_1\)は表の上半分の和をとって
\(p_1=0.45+0.12+0.03=\)\(0.60\)
同様に、前回投票の人が選ばれる確率\(p_2\)は一番左側の和をとって
\(p_2=0.45+0.10=\)\(0.55\)
(2)
今回棄権かつ前回投票の人の割合(母比率は)\(0.10\)。この分類以外の人の割合は\(0.90\)になるので、\(900\)人のうち今回棄権かつ前回投票の人数\(X\)は二項分布 \(B(900,0.10)\) に従う。
よって、
\(n=900,p=0.10\)
(3)
(2)より、\(X\)は\(B(900,0.10)\) に従うから
\(E(X)=900\cdot0.10=\)\(90\)
\(σ(X)=\sqrt{900\cdot0.10\cdot0.90}=\)\(9.0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→母平均の推定① back→母比率と標本比率