母平均の推定②(分散未知)

母集団の分散(標準偏差)が分からない場合の、母平均の推定方法について見ていきます。

・母平均の推定②(分散未知)
母平均が分からないので標本平均から母平均の推定をする訳ですが、前回扱った推定では母標準偏差の値が必要でした。しかし母平均が未知で母標準偏差が既知という状態は実際には少なく、母標準偏差も未知であることが多いです。そこでその場合は「\(n\)が十分大きい」という条件はつきますが次の標本標準偏差\(S\)で母標準偏差\(σ\)を代用することか可能です。

(標本標準偏差)
\(S=\sqrt{\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}(X_k-\overline{X})^2}\)

\(=\sqrt{\displaystyle\frac{1}{n}\{(X_1-\overline{X})^2+(X_2-\overline{X})^2+\cdots+(X_n-\overline{X})^2\}}\)

抽出した\(n\)個の標本の結果から標本平均\(\overline{X}\)を求めて、上記式により具体的に\(S\)を計算することが可能です。
もちろん代用できる理由はちゃんとあるのですがこれも高校範囲外なので、知識として知っておくとよいでしょう。
上記標本標準偏差の式は、数ⅠAのデータの分析で出てきた式と同じです。

よって\(S\)を用いた母平均\(m\)に対する信頼区間は、信頼度が\(95％\)のときは
\(\overline{X}-1.96\cdot\displaystyle\frac{S}{\sqrt{n}}≦m≦\overline{X}+1.96\cdot\displaystyle\frac{S}{\sqrt{n}}\)
となります。

(例題)
(1)太郎さんは、自分が住んでいる地域において、日曜日に晴れとなる確率を考えている。晴れの場合は\(1\)、晴れ以外の場合は\(0\)の値をとる確率変数を\(X\)と定義する。また、\(X=1\) である確率を\(p\)とすると、その確率分布は表\(1\)のようになる。

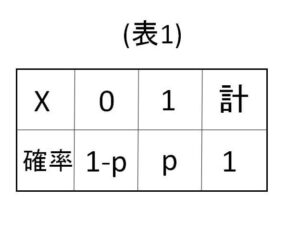
この確率変数\(X\)の平均(期待値)を\(m\)とすると
\(m=(ア)\) である。(ア)を\(p\)を用いて表せ。

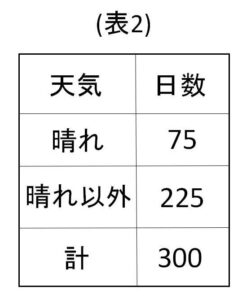
(2)太郎さんは、ある期間における連続した\(n\)週の日曜日の天気を、表\(1\)の確率分布をもつ母集団から無作為に抽出した大きさ\(n\)の標本とみなし、それらの\(X\)を確率変数\(X_1,X_2,\cdots,X_n\)で表すことにした。そして、その標本平均\(\overline{X}\)を利用して、母平均\(m\)を推定しようと考えた。実際に \(n=300\) として晴れの日数を調べたところ、表\(2\)のようになった。

(i)母標準偏差を\(σ\)とすると、\(n=300\)は十分に大きいので、標本平均\(\overline{X}\)は近似的に正規分布 \(N(m,(イ))\)に従う。(イ)を\(σ\)を用いて表せ。

(ii)一般に、母標準偏差\(σ\)がわからないとき、標本の大きさ\(n\)が大きければ、\(σ\)の代わりに標本の標準偏差\(S\)を用いてもよいことが知られている。\(S\)は
\(S=\sqrt{\displaystyle\frac{1}{n}\{(X_1-\overline{X})^2+(X_2-\overline{X})^2+\cdots+(X_n-\overline{X})^2\}}\)
\(=\sqrt{\displaystyle\frac{1}{n}(X_1^2+X_2^2+\cdots+X_n^2)-(ウ)}\)
で計算できる。(ウ)を\(\overline{X}\)を用いて表せ。

(iii)\(X\)は\(0\)または\(1\)の値をとることから
\(X_1^2=X_1\)、\(X_2^2=X_2\)、・・・\(X_n^2=X_n\)
が成り立つ。このことから(ii)の\(S\)はさらに変形でき、\(S=\sqrt{\overline{X}の式}\) で表される。この式を求めよ。

(iv)表\(2\)より、大きさ \(n=300\) の標本から求められる母平均\(m\)に対する信頼度\(95％\)の信頼区間を求めよ。

(解答)
(1)
(表\(1\))より
\(m=0\cdot(1-p)+1\cdot p\)
\(=p\)

(2)
(i)
(イ)は標本平均\(\overline{X}\)の分散なので
\((イ)=\displaystyle\frac{σ^2}{n}=\displaystyle\frac{σ^2}{300}\)

(ii)
\(S\)の根号の中身を整理すると
\(\displaystyle\frac{1}{n}\{(X_1-\overline{X})^2+(X_2-\overline{X})^2+\cdots+(X_n-\overline{X})^2\}\)
(展開すると)
\(=\displaystyle\frac{1}{n}(X_1^2+X_2^2+\cdots+X_n^2)-2\overline{X}\cdot\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}+\displaystyle\frac{(\overline{X})^2}{n}\cdot n\)

\(=\displaystyle\frac{1}{n}(X_1^2+X_2^2+\cdots+X_n^2)-2\overline{X}\cdot\overline{X}+(\overline{X})^2\)

\(=\displaystyle\frac{1}{n}(X_1^2+X_2^2+\cdots+X_n^2)-(\overline{X})^2\)

よって
\((ウ)=(\overline{X})^2\)

(iii)
(ii)と問題文より
\(S=\sqrt{\displaystyle\frac{1}{n}(X_1^2+X_2^2+\cdots+X_n^2)-(\overline{X})^2}\)
\(=\sqrt{\displaystyle\frac{1}{n}(X_1+X_2+\cdots+X_n)-(\overline{X})^2}\)
\(=\sqrt{\overline{X}-(\overline{X})^2}\)
\(=\sqrt{\overline{X}(1-\overline{X})}\)

(iv)
\(m\)に対する信頼度\(95％\)の信頼区間は\(σ\)を\(S\)で代用することにより
\(\overline{X}-1.96\cdot\displaystyle\frac{S}{\sqrt{300}}≦m≦\overline{X}+1.96\cdot\displaystyle\frac{S}{\sqrt{300}}\)

(iii)より
\(\overline{X}-1.96\cdot\sqrt{\displaystyle\frac{\overline{X}(1-\overline{X})}{300}}≦m≦\overline{X}+1.96\cdot\sqrt{\displaystyle\frac{\overline{X}(1-\overline{X})}{300}}\)

ここで(表\(2\))より晴れの日は\(75\)日、晴れ以外の日は\(225\)日で、それぞれ確率変数の値が\(1,0\)になることから
\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)

\(=\displaystyle\frac{75\cdot1+225\cdot0}{300}\)

\(=\displaystyle\frac{1}{4}\)

ゆえに
\(\displaystyle\frac{1}{4}-1.96\cdot\sqrt{\displaystyle\frac{\displaystyle\frac{1}{4}(1-\displaystyle\frac{1}{4})}{300}}≦m≦\displaystyle\frac{1}{4}+1.96\cdot\sqrt{\displaystyle\frac{\displaystyle\frac{1}{4}(1-\displaystyle\frac{1}{4})}{300}}\)

\(0.25-1.96\cdot\displaystyle\frac{1}{40}≦m≦0.25+1.96\cdot\displaystyle\frac{1}{40}\)

したがって信頼区間は
\(0.201≦m≦0.299\)

(参考)
(iv)より信頼区間は、\(300\)を\(n\)に戻して
\(\overline{X}-1.96\cdot\sqrt{\displaystyle\frac{\overline{X}(1-\overline{X})}{n}}≦m≦\overline{X}+1.96\cdot\sqrt{\displaystyle\frac{\overline{X}(1-\overline{X})}{n}}\)

(1)より \(m=p\) で、\(p\)は晴れの日の割合となるから母比率。
また、晴れの日(確率\(p\)で起こる)の場合には確率変数の値が\(1\)、晴れの日以外(確率\(1-p\))の場合には確率変数の値が\(0\)になるように設定しているので、標本平均\(\overline{X}\)はまさに標本比率\(R\)になる。よって不等式は
\(R-1.96\cdot\sqrt{\displaystyle\frac{R(1-R)}{n}}≦p≦R+1.96\cdot\sqrt{\displaystyle\frac{R(1-R)}{n}}\)

これは標本比率による母比率の推定の不等式である。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→母比率の推定　back→母平均の推定①