正規分布を利用する仮説検定について見ていきます。
・母平均の検定
得られたデータから、ある仮説が正しいかどうかを判断する統計的手法を仮説検定(統計的仮説検定)と呼びます。母平均の推定では
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}\)
において、\(Z\)が標準正規分布に従うことから \(-1.96≦Z≦1.96\) となる確率が\(95%\)であることを利用しましたが、逆に検定では \(Z≦-1.96,\ Z≧1.96\) となる確率が\(5%\)(稀に起こる)となることを利用します。
仮説検定の流れは数IAで扱ったものと同じです。(→(仮説検定) も参考にして下さい)
数ⅡBで扱う仮説検定は「母平均の検定・母比率の検定」ですが、まずは母平均の検定から具体例を挙げて考えたいと思います。
(例)
「ある食品メーカーの缶詰の内容量が\(50\mathrm{g}\)と表示してあった。これに疑問をもった\(A\)君が、表示に偽りがないかを調べるために無作為にこの缶詰を\(100\)個選んでその内容量を測定した結果、平均で\(49.6\mathrm{g}\)であった。この缶詰の内容量の標準偏差を\(2\mathrm{g}\)とするとき、缶詰の表示が誤りかどうかを判断せよ」
まずは対立仮説と帰無仮説を設定します。内容量の平均値を\(m(\mathrm{g})\)とすれば、\(A\)君は表示が誤りであることを主張したいので、次のようになります。
対立仮説\(H_1\):\(m≠50\)
帰無仮説\(H_0\):\(m=50\)
帰無仮説が正しいと仮定すると、標本平均\(\overline{X}\)は標本の大きさ\(100\)が十分大きいことから
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}\)・・・①
が標準正規分布に従うことになります。
ここで起きえないという確率は各個人によって若干感覚が異なるので、有意水準という基準を設定します。例えば有意水準を\(5%\)(\(0.05\))にすると、正規分布表により
\(P(-1.96≦Z≦1.96)=0.95\)
なので
\(Z≦-1.96,\ Z≧1.96\)・・・②
となる確率は\(5%\)です。②の範囲に①で計算した\(Z\)の値が含まれれば、それは\(5%\)以下の確率でしか起きえないことなので、帰無仮説で設定した\(m\)の値が妥当でないと判断できます。そこで②の範囲を棄却域とよびます。
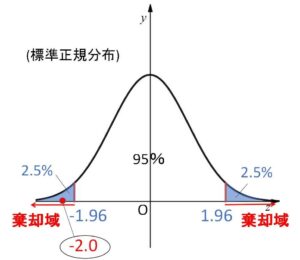
調査の結果などにより
\(\overline{X}=49.6\)、\(n=100\)、\(σ=2\)
また、帰無仮説により \(m=50\) だからこれらを①に代入すると
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}=\displaystyle\frac{49.6-50}{\displaystyle\frac{2}{\sqrt{100}}}=\)\(-2.0\)
したがって \(Z≦-1.96\) の範囲に\(-2.0\)が含まれていることから、帰無仮説は棄却され、対立仮説が採用されることになり、この例では内容量の表示は正しくないと結論づけることになります。
一方、有意水準を\(1%\)(\(0.01\))に設定すると
\(P(-2.58≦Z≦2.58)=0.99\)
なので棄却域は
\(Z≦-2.58,\ Z≧2.58\)・・・③
先ほど計算した \(-2.0\) という値は棄却域③に含まれないので、帰無仮説は棄却されないことになります。ここで、「帰無仮説が棄却されない=帰無仮説が正しい→対立仮説が間違い」 ということではないことに注意してください。その理由は例えば帰無仮説を別の設定 \(m=49.8\) や \(m=50.3\) などにしても、それぞれ \(Z=-1.0\)、\(Z=1.5\) となり棄却域③に含まれず、このように棄却域に含まれないような\(m\)がいくらでも存在するからです。帰無仮説はその名前「無に帰す」の通り最初から捨てるためだけに作られた仮説です。
よって、帰無仮説が棄却されない場合には帰無仮説が正しいという判断はできないため、対立仮説が正しいのか間違っているのか判断ができません。
(まとめ)
帰無仮説\(H_0\)を棄却する→対立仮説\(H_1\)は正しいと判断
帰無仮説\(H_0\)を棄却しない→対立仮説\(H_1\)が正しいかどうか分からない
その他の注意点としては・・・
(注1)
母標準偏差は分からないことも多いので、その場合は標本標準偏差で代用するのは推定の場合と同じ。(標本の大きさ\(n\)が十分大きいという条件は必要)
(注2)数IAとの対応
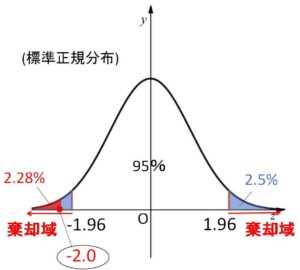
有意水準を\(5%\)とした最初の例題設定では
棄却域:\(Z≦-1.96,\ Z≧1.96\)
に \(Z=-2.0\) が含まれるので帰無仮説は棄却されるという判断でしたが、これを確率に対応させると
\(P(Z≦-1.96)=0.0250\) (\(2.5%\))
\(P(Z≦-2.0)=0.0228\) (\(2.28%\))
において、\(0.0250>0.0228\) と比べていることになります。
(注3)両側片側・片側検定
上記例では対立仮説を \(m≠50\) として\(m\)が\(50\)かそうでないかだけに着目して棄却域を正負の両側に設定したが、この\(50\)と比べて大小が明確な場合や大小について着目したい場合には、棄却域を片側だけに設定することもあります。これらの検定方法を前者が両側検定とよぶのに対し、後者を片側検定とよびます。
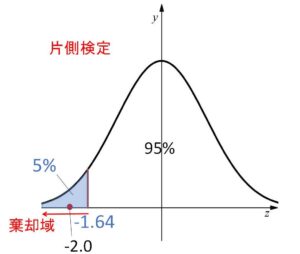
例えば、上記の例で有意水準を\(5%\)として片側検定すると、標本平均が \(\overline{X}=49.6<50\) であることから負の領域だけを考えることにして
対立仮説\(H_1\):\(m<50\)
帰無仮説\(H_0\):\(m=50\)
とすれば、\(P(Z≧-1.64)=0.95\) より
棄却域:\(Z≦-1.64\)
であり、\(Z=-2.0\) は棄却域に含まれるので帰無仮説は棄却されることになります。
・母比率の検定
母平均の検定と全く同じ方法で母比率の検定もすることができます。
ある性質\(A\)に着目したとき、母集団における性質\(A\)をもつ個体の割合を\(p\)(母比率)、集団から大きさ\(n\)の標本を抽出したとき、標本において性質\(A\)をもつ個体の割合を\(R\)(標本比率)とします。\(R\)は\(n\)が大きいとき近似的に正規分布 \(N(p,\sqrt{\displaystyle\frac{p(1-p)}{n}})\) に従うので
\(Z=\displaystyle\frac{R-p}{\sqrt{\displaystyle\frac{p(1-p)}{n}}}\)・・・(i)
の値を調べて、これが棄却域に入るかどうかを調べればよいです。
\(n\)と\(R\)は調査の結果から分かり、\(p\)は帰無仮説で設定する母比率の値です。これらを(i)に代入すればOKです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→仮説検定の過誤 back→母比率の推定