曲線上の点と直線の距離に関する問題について見ていきます。
(例題)
2点 \(A(0,-1)\),\(B(2,1)\) がある。点\(P\)が放物線 \(y=x^2\) 上を動くとき、\(△ABP\)の面積の最小値と、そのときの点\(P\)の座標を求めよ。
(解答)
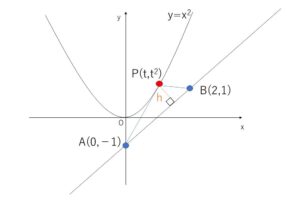
\(AB\)を底辺として考える。
\(AB=\sqrt{2^2+2^2}=2\sqrt{2}\)
また直線\(AB\)の方程式は
\(y+1=1(x-0)\) より \(x-y-1=0\)
\(P(t,t^2)\)とおくと、\(△ABP\)の高さ\(h\)は直線\(AB\)と点\(P\)の距離で
\(h=\displaystyle\frac{|t-t^2-1|}{\sqrt{1^2+1^2}}\)\(=\displaystyle\frac{|-t^2+t-1|}{\sqrt{2}}\)
よって
\(△ABP\)
\(=\displaystyle\frac{1}{2}・2\sqrt{2}・\displaystyle\frac{|-t^2+t-1|}{\sqrt{2}}\)
\(=|-t^2+t-1|\)
\(=|-(t-\displaystyle\frac{1}{2})^2-\displaystyle\frac{3}{4}|\) (平方完成した)
\(=(t-\displaystyle\frac{1}{2})^2+\displaystyle\frac{3}{4}\)
ゆえに \(△ABP\)は \(t=\displaystyle\frac{1}{2}\) のとき、最小値 \(\displaystyle\frac{3}{4}\) をとり、このとき \(P(\displaystyle\frac{1}{2},\displaystyle\frac{1}{4})\)
※直線\(AB\)に平行な直線を考えても解くことができます。
\(AB\)に平行な直線\(l\)上の任意の点と直線\(AB\)の距離は等しいので、\(l\)を\(y=x^2\)に近づけていくと、\(y=x^2\)の点で直線\(AB\)に最も近い点は、\(l\)が \(y=x^2\)上と一点で交わるとき(接するとき)の交点となることがわかります。
このとき、底辺を\(AB\)としたとき\(△ABP\)の高さ\(h\)が最小となるので、面積も最小となります。1点で交わるときの条件は判別式を使って求めることができます。
(別解)
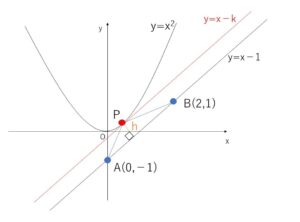
直線\(AB\)に平行な直線を考えると、この直線が \(y=x^2\)・・・①と1点で交わる(接する)ときに、\(AB\)を底辺としたときの高さ\(h\)が最小となるので、\(△ABP\)の面積が最小となる。
直線\(AB\)の方程式は \(y=x-1\) であり、平行な直線を\(y=x-k\)・・・②とおく
②を①に代入して
\(x-k=x^2\)
\(x^2-x+k=0\)・・・③
①と②が1点で交わるとき③は重解をもつので、
\(D=1-4k=0\) より \(k=\displaystyle\frac{1}{4}\)
このとき \(P\)の\(x\)座標は③の解(重解)なので、\(x=\displaystyle\frac{1}{2}\)
よって \(P(\displaystyle\frac{1}{2},\displaystyle\frac{1}{4})\)
また高さ\(h\)は、\(P\)と 直線\(AB\) \(x-y-1=0\) の距離なので
\(h=\displaystyle\frac{|\displaystyle\frac{1}{2}-\displaystyle\frac{1}{4}-1|}{\sqrt{1^2+1^2}}\)\(=\displaystyle\frac{3}{4\sqrt{2}}\)
したがって
\(△ABP=\displaystyle\frac{1}{2}AB・h\)\(=\displaystyle\frac{1}{2}・\sqrt{2^2+2^2}・\displaystyle\frac{3}{4\sqrt{2}}\)\(=\)\(\displaystyle\frac{3}{4}\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→直線と三角形の等分 back→三角形の面積