折れ線の長さの最小値を求めるには、対称な点を考えることがポイントとなります。
(例題1)
2点\(A(-1,3)\),\(B(5,11)\)がある。点\(Q\)が直線 \(y=2x\) 上にあるとき、\(QA+QB\)を最小にする点\(Q\)の座標を求めよ。
折れ線のままだと扱いにくいので、\(A,B\)の一方を\(l\)に関して対称移動させて、\(l\)に関して反対側にくるようにします。例えば\(B\)の\(l\)に関する対称な点\(B’\)を考えると、\(l\)上の任意の点\(Q\)について\(QB=QB’\)が成り立つので、\(QA+QB=QA+QB’\)
\(QA+QB’\)の最小値は、\(AQB’\)が一直線上にあるときなので、このときの\(Q\)の座標が求める答えとなります。
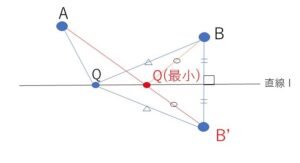
(解答)
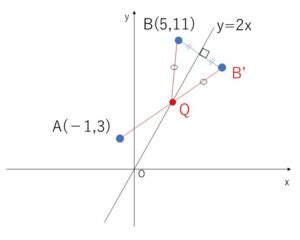
点\(A,B\)と\(y=2x\)の位置関係は図の通り。
\(B\)の \(y=2x\) に関する対称な点を\(B’\)とすると
\(QA+QB=AQ+QB’\)
よって\(QA+QB\)が最小になるときは、\(AQ+QB’\)が最小となるときで、このとき3点\(A,Q,B’\)は一直線上にある。
\(B'(a,b)\)とおいて\(B’\)の座標を求める。
\(BB’\)の中点が\(y=2x\)上にあるので
\(\displaystyle\frac{11+b}{2}=2・\displaystyle\frac{5+a}{2}\)
よって \(11+b=10+2a\)・・・①
また、直線\(BB’\)は\(y=2x\)と垂直なので、\(BB’\)の傾きが\(-\displaystyle\frac{1}{2}\)となり
\(\displaystyle\frac{b-11}{a-5}=-\displaystyle\frac{1}{2}\)
よって \(2b-22=-a+5\)・・・②
①②より
\(a=\displaystyle\frac{29}{5}\),\(b=\displaystyle\frac{53}{5}\) よって \(B'(\displaystyle\frac{29}{5},\displaystyle\frac{53}{5})\)
また\(Q\)は直線 \(y=2x\) と直線\(AB’\)の交点で、直線\(AB’\)の方程式は
\(y-3=\displaystyle\frac{\displaystyle\frac{53}{5}-3}{\displaystyle\frac{29}{5}+1}(x+1)\) より
\(y=\displaystyle\frac{19}{17}x+\displaystyle\frac{70}{17}\)・・・③
③と\(y=2x\)を連立させて解くと
\(Q(\displaystyle\frac{14}{3},\displaystyle\frac{28}{3})\)
(例題2)
\(A(5,1)\),\(B(2,6)\)とする。\(x\)軸上に点\(P\),\(y\)軸上に点\(Q\)をとるとき、\(AP+PQ+QB\)を最小にする点\(P,Q\)の座標を求めよ。また、そのときの最小値を求めよ。
(解答)
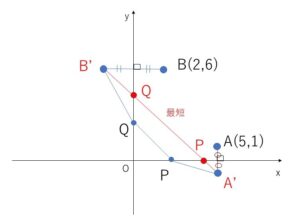
\(B\)の\(y\)軸に関する対称な点を\(B’\)、\(A\)の\(x\)軸に関する対称な点を\(A’\)とすると
\(B'(-2,6)\),\(A'(5,-1)\)
\(AP+PQ+QB\)\(=A’P+PQ+QB’\) であり
\(A’P+PQ+QB’\)が最小になるときは、4点\(A’,P,Q,B’\)が一直線上にあるときである。
直線\(A’B’\)の方程式は
\(y-6=\displaystyle\frac{-1-6}{5+2}(x+2)\) だから
\(y=-x+4\)
よって\(P(4,0)\),\(Q(0,4)\)
また最小値は2点\(A’,B’\)間の距離なので
(最小値)\(=\sqrt{(5+2)^2+(-1-6)^2}\)\(=\)\(7\sqrt{2}\)
※最小となるときに、4点\(A’,P,Q,B’\)が一直線上になることを丁寧に考えてみます。
まず2点\(P,Q\)が両方動くとすると難しいので、片方を固定します。
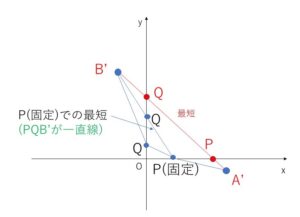
\(P\)を固定(動かない点)として(\(Q\)は動く点)、\(A’P+PQ+QB’\)の最小値を考えると、最小となるときには3点\(PQB’\)が一直線となるときです。よって、\(P→Q→B’\)の経路は、線分\(PB’\)のみを考えればよいことになります。
したがって、\(A’P+PQ+QB’\)が最小となるときは、\(A’P+PB’\)が最小となるときで、それは\(A’PB’\)が一直線上にあるときです。(このとき自動的に\(Q\)が決まり、\(Q\)は直線\(A’B’\)と\(y\)軸の交点となります)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→共線・共点① back→線分の垂直二等分線