共線・共点②(3直線の位置関係と三角形の有無)

3直線の位置関係と三角形の有無に関する問題について見ていきます。

(例題1)
\(x-2y=-5\)・・・①　\(3x+2y=-7\)・・・②　\(kx-y=1-k\)・・・③
で表される3直線がある。次の条件を満たすときの\(k\)の値、あるいは範囲をそれぞれ求めよ。
(1)3直線が1点で交わる　(2)3直線の交点が2個
(3)3直線の交点が3個

①②は1点で交わることから(1)~(3)は次の場合となります。
(1)①②の交点を③が通る
(2)①と③が平行で一致しない or ②と③が平行で一致しない
(3)①②に③が交わり、③が①②の交点を通らない　→③が①②と平行でなく、①②の交点を通らない→(1)(2)以外

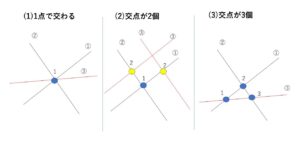
(2)については、一致すると交点が1個になってしまいます。

(解答)
(1)
①②の交点は連立し解くと \((-3,1)\)
③がこの交点を通ればよいので
\(-3k-1=1-k\)　よって　\(k=-1\)

(2)
③は \(y=kx+k-1\) だから　傾き\(k\)の直線
①の傾きは \(\displaystyle\frac{1}{2}\)、②の傾きは \(-\displaystyle\frac{3}{2}\)
①または②と平行で一致しないとき交点が2個となるので、
平行のとき \(k=\displaystyle\frac{1}{2},-\displaystyle\frac{3}{2}\)
このとき、\(k≠-1\)なので、③は①②の交点は通らず①②と一致しない。

答 \(k=\displaystyle\frac{1}{2},-\displaystyle\frac{3}{2}\)

(3)
交点が3個のとき、③が①②両方に交わり、かつ①②の交点を③が通らないときであり、それは③が①②に平行でなく、①②の交点を通らないときである。
よって(1)(2)以外の場合を考えればよく、
\(k<-\displaystyle\frac{3}{2}\), \(-\displaystyle\frac{3}{2}<k<-1\), \(-1<k<\displaystyle\frac{1}{2}\),  \(k>\displaystyle\frac{1}{2}\)

(例題2)
3直線 \(x-2y=-5\)・・・①　\(3x+2y=-7\)・・・②　\(kx-y=1-k\)・・・③
が三角形を作らないときの\(k\)の値を求めよ。

3直線が三角形を作らないときは次の通り。

なお本問は①②が平行でないので、3直線が平行の場合は考えなくてよいです。

(解答)
①②は平行でなく、1点で交わる。
3直線が三角形を作らないときは
(i)①②の交点を③が通る
(ii)①と③が平行　または　②と③が平行

(i)
①と②の交点は連立して解くと \((-3,1)\)
③がこの点を通るので
\(-3k-1=1-k\)　よって　\(k=-1\)

(ii)
①②の傾きはそれぞれ、 \(\displaystyle\frac{1}{2}\), \(-\displaystyle\frac{3}{2}\)
③の傾きは\(k\)なので
\(k=\displaystyle\frac{1}{2},-\displaystyle\frac{3}{2}\)

以上より三角形を作らないのは \(k=-1,\displaystyle\frac{1}{2}\)\(,-\displaystyle\frac{3}{2}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2直線の方程式を表す条件　back→共線・共点①