円と直線の交点を通る円

円と直線の交点を通る図形に関する問題についてみていきます。
今回も \(kf(x,y)+g(x,y)=0\) を用いていきます。

(例題)
円 \((x-4)^2+(y-3)^2=21\) と 直線 \(y=mx\) とが2交点をもち、その2交点を通る円のうちに\(x\)軸と\(y\)軸の両方に接するものがあるという。この条件をみたす\(m\)の値をすべて求めよ。

(解答)

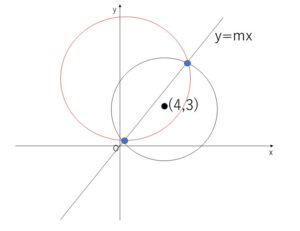
まず円と直線が2点で交わる条件を考える。
\((x-4)^2+(y-3)^2=21\) に \(y=mx\) を代入して
\((x-4)^2+(mx-3)^2=21\)
展開して整理すると
\((m^2+1)x^2-2(3m+4)x+4=0\)

この\(x\)の2次方程式が異なる2つの実数解をもつ条件は
\(\displaystyle\frac{D}{4}>0\)
\((3m+4)^2-4(m^2+1)>0\)
\(5m^2+24m+12>0\)・・・①

次に
\((x-4)^2+(y-3)^2-21\)\(+k(mx-y)\)\(=0\)・・・(A)
を考えると、(A)は①の条件を満たすとき、円と直線の交点を通る円を表す。
(A)より
\(x^2-(mk+8)x+y^2+(k-6)y\)\(+4\)\(=0\)
平方完成して
\((x-\displaystyle\frac{mk+8}{2})^2+(y+\displaystyle\frac{k-6}{2})^2\)\(=(\displaystyle\frac{mk+8}{2})^2+(\displaystyle\frac{k-6}{2})^2\)\(-4\)・・・(B)

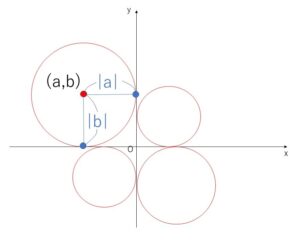
(B)は\(x\)軸と\(y\)軸に接するから
\(|\displaystyle\frac{mk+8}{2}|=|-\displaystyle\frac{k-6}{2}|\)\(=\sqrt{(\displaystyle\frac{mk+8}{2})^2+(\displaystyle\frac{k-6}{2})^2-4}\)

すべての辺は\(0\)以上の値なので2乗して
\((\displaystyle\frac{mk+8}{2})^2=(\displaystyle\frac{k-6}{2})^2\)\(=(\displaystyle\frac{mk+8}{2})^2+(\displaystyle\frac{k-6}{2})^2-4\)・・・(C)

(C)の左辺と右辺より
\((\displaystyle\frac{mk+8}{2})^2\)\(=(\displaystyle\frac{mk+8}{2})^2+(\displaystyle\frac{k-6}{2})^2-4\) より
\((\displaystyle\frac{k-6}{2})^2-4=0\)
これを解くと \(k=2,10\)

(C)の左辺と中辺より
\(k=2\)のとき
\((\displaystyle\frac{2m+8}{2})^2=(-2)^2\)
これを解くと \(m=-2,-6\)
\(k=10\)のとき
\((\displaystyle\frac{10m+8}{2})^2=2^2\)
これを解くと \(m=-\displaystyle\frac{2}{5},-\displaystyle\frac{6}{5}\)

このうち \(5m^2+24m+12>0\)・・・① を満たすのは
\(m=-6,-\displaystyle\frac{2}{5}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円上の動点と円上にない定点の距離　back→2円の交点を通る直線・円