円上を動く点と、円上にない定点の距離の最小値に関する問題について見ていきます。
ポイントは円の中心と定点を結ぶ直線です。
(例題1)
\(xy\)平面上における点 \((5,6)\)と 円 \(x^2+y^2+2x+4y-20=0\) 上の点との最短距離を求めよ。
(解答)
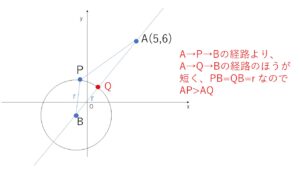
円上をぐるぐると点\(P\)が動いたときに、\(A(5,6)\)との距離の最小値はいくらになるかという問題ですが、\(A(5,6)\)と中心を結ぶ直線を考えて、その直線と円の交点の\(A\)に近い方を\(Q\)とすると、それ以外の円上の点では\(Q\)のときよりも距離は長くなります。
なぜなら、円の中心を\(B\)とすると \(AP+PB≧AB\)・・・① ,\(AB=AQ+QB\)であり、円の半径を\(r\)とすれば ①は \(AP+r≧AQ+r\) だから
\(AP≧AQ\) となるからです。
円\(x^2+y^2+2x+4y-20=0\) は
\((x+1)^2+(y+2)^2=25\)
点\(A(5,6)\)はこの円の外側にあり、\(A\)と最も距離が短くなる円周上の点\(Q\)は、\(A\)と円の中心\(B(-1,-2)\)を結んだ直線と円の交点のうち\(A\)に近い方である。
\(AQ=AB-BQ\) であり
\(AB=\sqrt{6^2+8^2}=10\), \(BQ=5\)(円の半径) なので
\(AQ=10-5=5\)
最小値は \(5\)
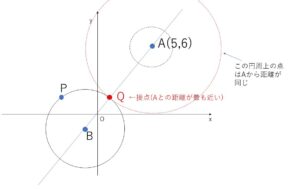
\(A(5,6)\)を中心とする円を考えて徐々に半径を大きくしていくと、円が中心から等距離にある点の集合であることに着目すれば、この円と問題で与えられた円が外接するときの接点が最も\(A\)に近い円周上の点であることがわかります。接点は2円の中心を結ぶ直線上にあるので、この場合も結局直線\(AB\)を考えることになります。
(例題2)
円 \(x^2+y^2=1\) 上の点\(P\)と、直線 \(16x-12y=25\) 上の点\(Q\)との距離\(PQ\)の最小値を求めよ。
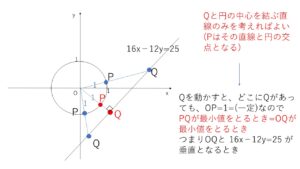
両方動かすと大変なので、まず外部の点を固定します。すると(例題1)よりその固定された点との最小値をとる円周上の点は、\(Q\)と円の中心\(O\)を結ぶ直線上にあります。よって直線\(16x-12y=25\)上で点\(Q\)がどこにあっても円の中心と結ぶ直線を考えればよいことになります。
そして最後に\(Q\)を動かします。\(PQ\)が最小となるのは、円の中心と\(Q\)を結ぶ直線が、\(16x-12y=25\)に垂直になるときです。(このとき\(OQ\)が最小となるから、\(PQ\)も最小となります)
(解答)
直線\(16x-12y=25\)上の1点\(Q\)をとり固定する。このとき\(PQ\)が最小となるときは、\(OQ\)上に\(P\)がある。よって以下\(P\)に関しては\(OQ\)と円との交点だけを考えればよい。
次に\(Q\)を動かすと、どこに\(Q\)があっても\(OP=1\)なので、\(PQ\)が最小となるときは\(OQ\)が最小となるときで、このとき\(PQ\)は \(O(0,0)\)と直線 \(16x-12y=25\) の距離を\(d\)とすると\(d-1\)である。
したがって\(PQ\)の最小値は
\(d-1=\displaystyle\frac{|0-0-25|}{\sqrt{16^2+12^2}}-1\)\(=\displaystyle\frac{25}{20}-1\)\(=\)\(\displaystyle\frac{1}{4}\)
(別解)
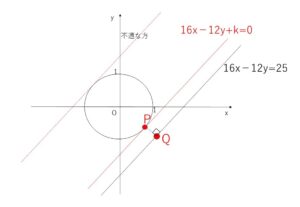
直線\(16x-12y=25\) を平行移動させて円に近づけていくと、\(PQ\)が最小となる\(P\)は、直線と円が初めて接するときの接点となる。
\(16x-12y+k=0\)・・・① が \(x^2+y^2=1\) と接するとき
\(\displaystyle\frac{|k|}{\sqrt{16^2+12^2}}=1\)
よって
\(k=±20\)
このうち、\(k=20\)は \(16x-12y=25\) に近い方の接線ではないので不適。
\(PQ\)の最小値は
\(16x-12y-20=0\)・・・① と \(16x-12y=25\)・・・② の距離となるので
①上の点 \((\displaystyle\frac{5}{4},0)\) と②の距離を考えて
\(\displaystyle\frac{|20-0-25|}{\sqrt{16^2+12^2}}\)\(=\displaystyle\frac{5}{20}\)\(=\)\(\displaystyle\frac{1}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→放物線と円の共有点 back→円と直線の交点を通る円