動点が絡む軌跡の問題について見ていきます。
(例題1)
点\(P\)が放物線 \(y=x^2\) の上を動くとき、点\(A(1,2)\) と\(P\)とを結ぶ線分\(AP\)を\(2:1\)の比に内分する点の軌跡を求めよ。
あとは条件から\(s,t\)を消去することにより、\(x,y\)の方程式を導きます。
(解答)
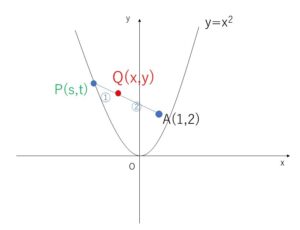
点\(P\)を\((s,t)\)とおくと、これが \(y=x^2\) 上にあるので
\(t=s^2\)・・・①
また、線分\(AP\)を\(2:1\)の比に内分する点を \(Q(x,y)\) とおくと
\(x=\displaystyle\frac{1+2s}{3}\)・・・②
\(y=\displaystyle\frac{2+2t}{3}\)・・・③
②③から \(s=・・・\), \(t=・・・\) として①に代入します。
②より \(s=\displaystyle\frac{3x-1}{2}\)・・・④
③より \(t=\displaystyle\frac{3y-2}{2}\)・・・⑤
④⑤を①に代入して
\(\displaystyle\frac{3y-2}{2}=(\displaystyle\frac{3x-1}{2})^2\)・・・(※)
整理して
\(y=\displaystyle\frac{3}{2}x^2-x+\displaystyle\frac{5}{6}\)・・・⑥
また逆に⑥上の点は条件を満たす。
答 放物線 \(y=\displaystyle\frac{3}{2}x^2-x+\displaystyle\frac{5}{6}\)
\(s\)の範囲も念のため確認しておくと、\(s=\displaystyle\frac{3x-1}{2}\)より\(x\)がすべての実数をとれば、\(s\)もすべての実数をとるので、問題ありません。
(別解)媒介変数(1文字)による解法
1つ目の解法では\(P\)の座標を2文字\(s,t\)を使って表しましたが、1文字で表しても解けます。
\(P\)の\(x\)座標を\(s\)とおくと \(y=x^2\) にあるから \(P(s,s^2)\)とおける。
また、線分\(AP\)を\(2:1\)の比に内分する点を \(Q(x,y)\) とすると
\(x=\displaystyle\frac{1+2s}{3}\)・・・(A)
\(y=\displaystyle\frac{2+2s^2}{3}\)・・・(B)
(A)より、\(s=\displaystyle\frac{3x-1}{2}\)
(B)に代入して
\(y=\displaystyle\frac{2}{3}(\displaystyle\frac{3x-1}{2})^2+\displaystyle\frac{2}{3}\)
整理して
\(y=\displaystyle\frac{3}{2}x^2-x+\displaystyle\frac{5}{6}\)・・・(C)
また逆に(C)上の点は条件を満たす。
答 放物線 \(y=\displaystyle\frac{3}{2}x^2-x+\displaystyle\frac{5}{6}\)
(例題2)
\(x,y\)平面上に原点\(O(0,0)\)を中心とする半径\(1\)の円\(C\)とその上の点\(A(1,0)\)がある。円\(C\)上を動く点\(P\)に対して、3点\(O,A,P\)が三角形を作るとき、その三角形の重心を\(G\)とする。\(G\)の軌跡を求めよ。
(解答)
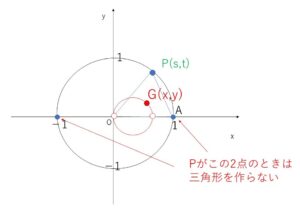
円\(C\)上の点\(P\)を\(P(s,t)\) とおくと、
\(s^2+t^2=1\)・・・①
また\(△OAP\)の重心を\(G(x,y)\)とおくと
\(x=\displaystyle\frac{0+1+s}{3}\)・・・②
\(y=\displaystyle\frac{0+0+t}{3}\)・・・③
②より \(s=3x-1\)
③より \(t=3y\)
①に代入して
\((3x-1)^2+(3y)^2=1\)
両辺\(9\)で割って
\((x-\displaystyle\frac{1}{3})^2+y^2=\displaystyle\frac{1}{9}\)・・・④
「\(△OAP\)が存在する→重心\(G\)は②③で表される」は正しいのですが、
「\((x,y)\)が②③で表される→\(△OAP\)が存在して\((x,y)\)は重心である」が必ずしも成り立たないことが原因となっています。
ここで、\(OAP\)が一直線上にあるとき\(△OAP\)は存在せず、このとき\(P\)は\((1,0)\),\((-1,0)\) である。
よって④上の点から ②③より (\(\displaystyle\frac{2}{3},0)\),\((0,0)\) の2点を除いたものが軌跡となる。
答 円 \((x-\displaystyle\frac{1}{3})^2+y^2=\displaystyle\frac{1}{9}\) (\((\displaystyle\frac{2}{3},0)\),\((0,0)\)を除く)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→媒介変数と軌跡 back→軌跡と逆の確認(十分性の確認)