動く2直線の交点の軌跡に関する問題について見ていきます。
(例題)
次の2直線の交点の軌跡を(1)(2)の場合に求めよ。
\(x+t(y-3)=0\)・・・① \(tx-(y+3)=0\)・・・②
(1)\(t\)が実数全体
(2)\(t≧0\)
交点を\(P(x,y)\)とすると、\(x,y\)は①②を満たすので、①②が軌跡の条件そのものとなります。①②よりつなぎの文字\(t\)を消去して\(x,y\)の関係式を導きます。なお消去する際には場合分けが必要となってきます。
(解答)
(1)
(ア)\(x≠0\) のとき ②より \(t=\displaystyle\frac{y+3}{x}\)
①に代入して
\(x+\displaystyle\frac{y+3}{x}(y-3)=0\)
整理すると
\(x^2+y^2=9\)・・・③
③より \(x=0\)のときは \(y=±3\) なので
\((0,3)\),\((0,-3)\)は除かれる。
(イ)\(x=0\)のとき
②より \(y=-3\)
このとき①より \(t=0\) とすればよい。
以上から軌跡は
円 \(x^2+y^2=9\) (\((0,3)\)を除く)
今軌跡を求めるのに\(t\)を消去しましたが、それは①②は平行ではないので交点は存在することから、
「\(t\)が任意のある実数値をとる→それに対応する①②の交点\((x,y)\)が存在」
という考え方であり、これを逆にとらえれば
「①②の交点\((x,y)\)が存在する→それに対応する実数\(t\)が存在」
となるので、円 \(x^2+y^2=9\) (\((0,3)\)を除く) 上の点に対応する\(t\)はすべての実数値となります。
(別解1)図形的に考える方法
\(x+t(y-3)=0\)・・・① \(tx-(y+3)=0\)・・・② について
\(t≠0\) のとき
①は傾き \(-\displaystyle\frac{1}{t}\)、定点\(A(0,3)\)を通る直線で
②は傾き \(t\), 定点\(B(0,-3)\)を通る直線であり
①②は垂直となる。
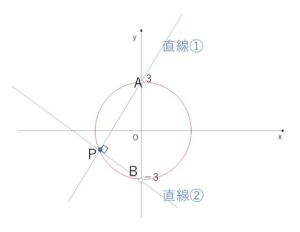
交点を\(P\)とすれば、\(\angle APB=90°\) なので
\(P\)は直径を\(AB\)とする円上にある。
ただし、\(t≠0,\displaystyle\frac{1}{t}≠0\) より点\(A,B\)は除く。
\(t=0\)のときは
①②より \(x=0\), \(y=-3\) となる。(点\(B\)となる)
したがって軌跡は、中心が原点,半径\(3\)の円から1点を除いたものだから
円 \(x^2+y^2=9\) (\((0,3)\)を除く)
(2)
(1)で実数全体を動くときの軌跡は円(1点を除く)と求めたのでこれの一部となります。\(t≧0\)の条件から、\(x\)や\(y\)の範囲について考えていきます。
\(t≧0\)のときの軌跡は(1)で求めた軌跡の一部(または全部)となる。
\(x+t(y-3)=0\)・・・① \(tx-(y+3)=0\)・・・② において
(ア)\(t=0\) のとき
①②より \(x=0\),\(y=-3\)
(イ)\(t>0\)のとき
\(y≠3\)のとき①より
\(t=\displaystyle\frac{x}{3-y}\)
\(x^2+y^2=9\) 上において \(3-y>0\) より
\(x>0\) となる。
また、\(y=3\) とすると ①より \(x=0\)。しかし\(x=0,y=3\)は②を満たさないので不適。
したがって求める軌跡は
円 \(x^2+y^2=9\) の \(x>0\)の部分と \((0,-3)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→弦の中点の軌跡 back→角の二等分線・線対称な図形