2接線の交点の軌跡の問題について見ていきます。
(例題)
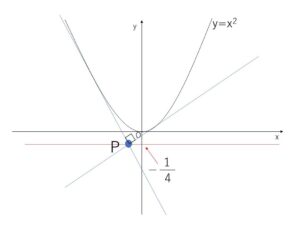
座標平面上の点\(P\)から放物線 \(y=x^2\) へ2本の接線が引けて、かつ、この2本の接線が直交するような点\(P\)の軌跡を求めよ。
\(P(s,t)\)とおく。
\(x\)軸に垂直な直線 \(x=s\) は接線とはなりえないので、接線の方程式は傾きを\(m\)として
\(y=m(x-s)+t\)・・・① とおける。
①を\(y=x^2\) に代入して\(x\)について整理すると
\(x^2-mx+ms-t=0\)・・・②
①と放物線が接するので②の判別式について \(D_1=0\)
よって
\(m^2-4(ms-t)=0\)
\(m\)について整理して
\(m^2-4sm+4t=0\)・・・③
\(m\)の2次方程式③の解が接線の傾きであり、2本の接線がひけて直交するためには、
③が2つの異なる実数解をもち、かつ2解を\(m_1,m_2\) とすると、\(m_1m_2=-1\)・・・④
③の判別式 \(D_2>0\) だから
\(\displaystyle\frac{D}{4}=4s^2-4t>0\)
よって \(s^2-t>0\)・・・⑤
また解と係数の関係から③の2解\(m_1,m_2\)について④より
\(4t=-1\)
よって \(t=-\displaystyle\frac{1}{4}\)・・・⑥
⑥より \(s^2-t=s^2+\displaystyle\frac{1}{4}>0\) だから
⑤を満たす。
したがって点\(P\)の軌跡は⑥より
\(y=-\displaystyle\frac{1}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対称移動と曲線の方程式 back→反転