直線や曲線の通過領域を求める問題について見ていきます。
(例題)
\(a\)を定数とする。直線 \(y=(2a+1)x-a^2-a\)・・・① について、\(a\)がすべての実数値をとって変わるとき、直線①の通過する領域を図示せよ。
\(a=-3\)のとき、①は \(y=-5x-6\)
・・・・ と\(a\)を変化させると①は色々な直線を表しますが、それら全部をあわせた領域を図示せよという問題です。
(解法1)順像法
\(y=(2a+1)x-a^2-a\)・・・① の右辺には\(x,a\)と文字が2つあるので、\(a\)を動かすために\(x\)を固定、つまり\(x\)を定数として扱います。\(x=k\) とすると①は \(y=(2a+1)k-a^2-a\)。 これは変数\(a\)1文字の関数となり、\(a\)を変化させたときに\(y\)がどのような値をとるか調べるのは簡単です。
\(y=(2a+1)x-a^2-a\)・・・① について\(x=k\) のときの\(y\)のとりうる値の範囲を調べる。
\(y=(2a+1)k-a^2-a\) を\(a\)について整理すると
\(y=-a^2+(2k-1)a+k\)
平方完成して
\(y=-(a-\displaystyle\frac{2k-1}{2})^2\)\(+k^2+\displaystyle\frac{1}{4}\)・・・②
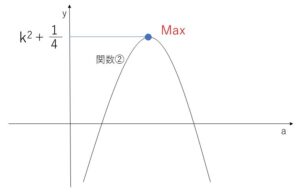
②は\(a\)の2次関数で、グラフは上に凸。
\(a\)はすべての実数値をとり、②の最大値が \(k^2+\displaystyle\frac{1}{4}\) であることから、
\(y≦k^2+\displaystyle\frac{1}{4}\)
他の全ての\(x=k\)についても同じことが言えるので、\(k\)を\(x\)に戻すと求める領域は
\(y≦x^2+\displaystyle\frac{1}{4}\)
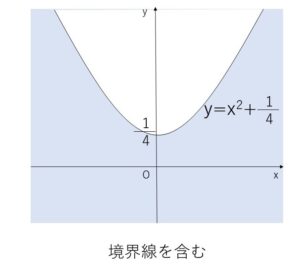
ほかの無数の\(x=k\)についても同様に線状になり、それぞれ1ラインずつ考えたものを合わせた領域が答えです。この考えかたを、ファックスを送信する際に1ラインずつ情報を処理することに由来してファクシミリの原理と呼ばれています。
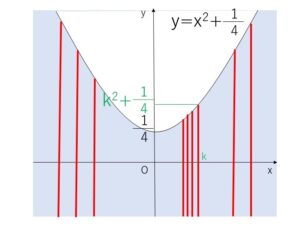
(解法2)逆像法
例えば、点\((1,1)\)を通るときの\(a\)の値を求めてみます。
\(y=(2a+1)x-a^2-a\)・・・① に代入すると、
\(1=2a+1-a^2-a\) \(a(a-1)=0\) より \(a=0,1\)。よって\((1,1)\)に対応する\(a\)として\(0,1\)が存在するので\((1,1)\)は①が通過する点です。
しかし点\((1,3)\)を通るときの\(a\)の値は、\(3=2a+1-a^2-a\)
\(a^2-a+2=0\) より \(a=\displaystyle\frac{1±\sqrt{7}i}{2}\)となり、対応する\(a\)が実数ではないので、\((1,3)\)は①が通過しない点となります。
1つ1つ点を調べていても仕方が無いので点を\((X,Y)\)と文字で置いて、これに対応する実数\(a\)が存在すればよいので、\(Y=(2a+1)X-a^2-a\) が実数解\(a\)をもつ条件を考えます。
①の\(x\)を\(X\),\(y\)を\(Y\)とおくと
\(Y=(2a+1)X-a^2-a\)
\(a\)について整理すると
\(a^2+(-2X+1)a-X+Y=0\)・・・③
\(a\)の2次方程式③が実数解をもつ条件は
\(D≧0\)
\((-2X+1)^2-4(-X+Y)≧0\)
整理すると
\(Y≦X^2+\displaystyle\frac{1}{4}\)
したがって求める領域は
\(y≦x^2+\displaystyle\frac{1}{4}\) (図は解法1と同じため省略)
※
順像法: \(a\)に対応する\((x,y)\)を定める
逆像法: \((x,y)\)に対応する\(a\)がある
と考え方の出発点はそれぞれ\(a\),\((x,y)\)と異なりますが、この問題では最終的には着目している文字はどちらも\(a\)です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→通過領域② back→命題と領域