連立不等式の表す領域について見ていきます。
(例題1)
連立不等式
\(
\begin{eqnarray} \left\{ \begin{array}{l} 1≦x^2 + y^2≦4 \\ x + y ≧1 \end{array} \right. \end{eqnarray}
\)
で表される領域を図示せよ。
「\(1≦x^2+y^2≦4\) かつ \(x+y≧1\)」です。よって両方を満たす領域、つまり両方の共通部分が答えとなります。なお最初の不等式はさらに分解すると、\(1≦x^2+y^2\) かつ \(x^2+y^2≦4\) です。
(解答)
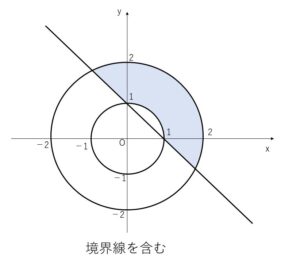
\(1≦x^2+y^2≦4\) の表す領域は
原点を中心とする半径\(1\)の円と半径\(2\)の円の間の部分。
また、\(x+y≧1\)の表す領域は、 \(y≧-x+1\)より 直線 \(y=-x+1\) より上側の部分。
どちらも境界線を含み、図にすると次の通り。
(例題2)
\(x,y\)の不等式
\(x^2+y^2-1≦0\)・・・① \(x^2-2x+y^2≦0\)・・・② について
①②を同時に満たす点\((x,y)\)の存在する範囲を図示して、その面積を求めよ。
(解答)
①は \(x^2+y^2≦1\)
②は \((x-1)^2+y^2≦1\)
\(x^2+y^2=1\)・・・③ と \(x^2-2x+y^2=0\)・・・④ の交点は
③-④より \(x=\displaystyle\frac{1}{2}\) ③より \(y=±\displaystyle\frac{\sqrt{3}}{2}\)
したがって図示すると次の通り。
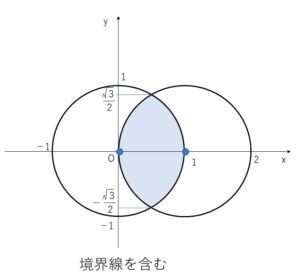
図示した図形は\(x\)軸について対称なので上側半分だけ考えます。
下図のように\(A,B,C\)をとると、\(\sin60°=\displaystyle\frac{\sqrt{3}}{2}\) より \(\angle B=60°\)。\(B,C\)は円の中心なので、\(BA=CA=1\)より \(\angle C=60°\)。よって\(△ABC\)は正三角形です。
上半分の図形は、正三角形\(ABC\)と緑色の部分2つで出来ていて、緑色1つは扇形\(ABC\)から正三角形\(ABC\)を除いた図形です。
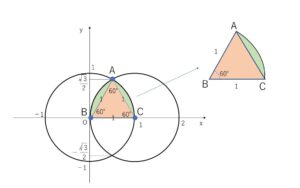
面積については、図示した図形は\(x\)軸について対称より上半分を考える。
図のように\(A,B,C\)を設定すると、\(\angle B=60°\)
\(BA=CA=1\) より \(\angle C=60°\) だから、\(△ABC\)は正三角形。
上半分の図形は、正三角形と緑色の部分2個を合わせたもので、緑色の部分の面積を\(S_1\)とすると
\(S_1=1^2・π・\displaystyle\frac{60°}{360°}\)\(-\displaystyle\frac{1}{2}・1・1・\sin60°\)\(=\displaystyle\frac{π}{6}-\displaystyle\frac{\sqrt{3}}{4}\)
よって上半分の面積は
\(△ABC+2S_1\)
\(=\displaystyle\frac{\sqrt{3}}{4}+2(\displaystyle\frac{π}{6}-\displaystyle\frac{\sqrt{3}}{4})\)\(=\displaystyle\frac{π}{3}-\displaystyle\frac{\sqrt{3}}{4}\)
したがって求める面積は
\(2(\displaystyle\frac{π}{3}-\displaystyle\frac{\sqrt{3}}{4})\)
\(=\)\(\displaystyle\frac{2π}{3}-\displaystyle\frac{\sqrt{3}}{2}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→不等式の表す領域②(絶対値) back→不等式の表す領域①(基礎)