絶対値を含む不等式の表す領域について見ていきます。
(例題)次の不等式で表される領域を、それぞれ\(xy\)平面に図示せよ。
(1)\(y≦|x-1|\)
(2)\(|x+y|<1\)
(3)\(|x|+|y|≦1\)
(4)\(|x-2|+|y-1|≦1\)
(5)\(|x-y|+|x+y|>2\)
(解答)
(1)
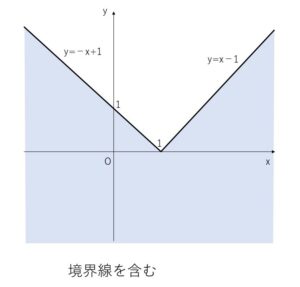
\(y≦|x-1|\) について
\(x<1\) のとき \(y≦-(x-1)=-x+1\)
\(x≧1\) のとき \(y≦x-1\)
(2)
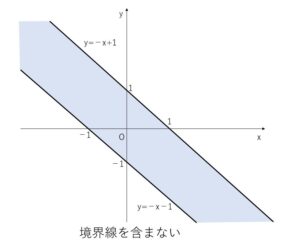
\(|x+y|<1\) より
\(-1<x+y<1\)
よって
\(y>-x-1\) かつ \(y<-x+1\)
(3)
正負で場合分けするなら、\(x,y\)それぞれ2通りずつの合計2×2=4通りになります。
それでも解けますが対称性に着目すると、①を満たす\((x,y)\)について、\(y\)軸対称の点 \((-x,y)\) も \(|-x|+|y|\)\(=|x|+|y|≦1\) より \(|-x|+|y|≦1\) となるので①を満たす点となることがわかります。同様に、\(x\)軸対称な点\((x,-y)\),原点対称な点\((-x,-y)\) も①を満たす点なので、\(x≧0\),\(y≧0\) のみ(第1象限の部分)を考えて、あとは折り返してやればよいことがわかります。
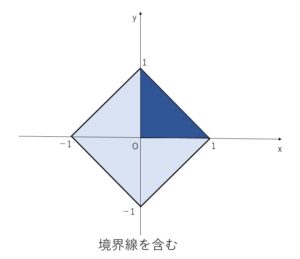
\(|x|+|y|≦1\) の表す領域は、\(x,y\)軸、原点について対称である。
\(x≧0\),\(y≧0\) を考えると
\(x+y≦1\) より \(y≦-x+1\)
よって次の通りとなる。
(4)
曲線の移動と同様に、\(f(x,y)>0\) を満たす点を\(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ平行移動させると、新たな領域は \(f(x-p,y-q)>0\) となります(証明は曲線の移動のときと同様です)。不等号の向きが逆でも同じです。
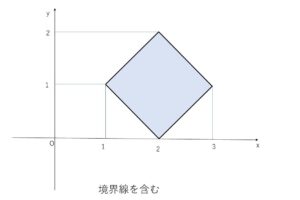
よって(3)の結果を利用すると、\(|x|+|y|≦1\) を \(x\)軸方向に\(2\),\(y\)軸方向に\(1\)だけ平行移動させたものを考えればよいことになります。
\(|x|+|y|≦1\) を \(x\)軸方向に\(2\),\(y\)軸方向に\(1\)だけ平行移動させたものである。よって(3)より領域は次の通り。
(5)
②を満たす\((x,y)\)と\(y\)軸対称な点\((-x,y)\)は、
\(|-x-y|+|-x+y|\)\(=|x+y|+|x-y|\)\(>2\) より、\(|-x-y|+|-x+y|\)\(>2\)となるので、②を満たします。\((x,-y)\),\((-x,-y)\) も同様に②を満たす点です。よって②が表す領域は\(x,y\)軸,原点対称なものです。
したがって\(x≧0\),\(y≧0\) について考えて折り返せばよいことになります。
②の\(|x+y|\)の部分は\(0\)以上なのでそのまま絶対値がはずれ、\(|x-y|\)の部分は\(x≧y\) と \(x<y\) で場合分けします。
\(|x-y|+|x+y|>2\)・・・② を満たす\((x,y)\)と\(y\)軸対称な点\((-x,y)\)は、
\(|-x-y|+|-x+y|\)\(=|x+y|+|x-y|\)\(>2\) より、\(|-x-y|+|-x+y|\)\(>2\)となるので、②を満たす。また\((x,-y)\),\((-x,-y)\) も同様に②を満たす。
よって②が表す領域は、\(x,y\),原点について対称である。
\(x≧0\),\(y≧0\)について考えると②は
\(|x-y|+x+y>2\)
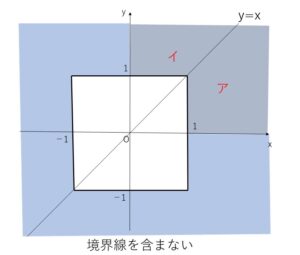
(ア)\(x≧y\) のとき
\(x-y+x+y>2\) より
\(x>1\)
(イ)\(x<y\) のとき
\(-(x-y)+x+y>2\) より
\(y>1\)
以上から表す領域は次の通り。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→不等式の表す領域③(積の形) back→連立不等式の表す領域