積の形で表された不等式の表す領域について見ていきます。
(例題)次の不等式の表す領域を図示せよ。
(1) \((y-x^2)(-x+y-2)\)\(≧0\)
(2) \(2x^2+xy-y^2-4x+2y\)\(<0\)
(3) \(xy(x^2+y^2-1)\)\(>0\)
(解答)
(1)
「\(a≧0\) かつ \(b≧0\) または \(a≦0\) かつ \(b≦0\)」(\(a,b\)がどちらも正かどちらも負) となります。よって与式は
「\(y-x^2≧0\) かつ \(-x+y-2≧0\)・・・① または \(y-x^2≦0\) かつ \(-x+y-2≦0\)・・・②」となり、「または」なので ①② を合わせた領域が答えとなります。
与えられた不等式は
\(y-x^2≧0\) かつ \(-x+y-2≧0\)・・・①
または
\(y-x^2≦0\) かつ \(-x+y-2≦0\)・・・②
と同値。
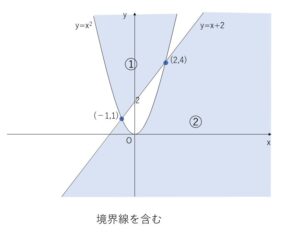
①は \(y≧x^2\) かつ \(y≧x+2\)
②は \(y≦x^2\) かつ \(y≦x+2\)
\(y=x^2\) と \(y=x+2\) の交点を連立して求めると
\((-1,1)\), \((2,4)\)
以上より図示すると次の通り。
(2)
\(2x^2+xy-y^2-4x+2y\)\(<0\) より \(x\)について整理すると
\(2x^2+(y-4)x-y^2+2y<0\)
\(2x^2+(y-4)-y(y-2)<0\)
よって
\((2x-y)(x+y-2)\)\(<0\)
したがって
\(2x-y>0\) かつ \(x+y-2<0\)・・・①
または
\(2x-y<0\) かつ \(x+y-2>0\)・・・②
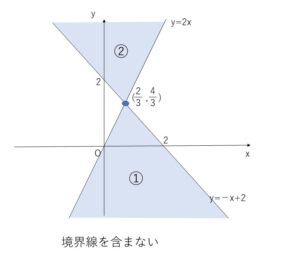
①は \(y<2x\) かつ \(y<-x+2\)
②は \(y>2x\) かつ \(y>-x+2\)
\(y=2x\) と \(y=-x+2\) の交点は連立して求めると
\((\displaystyle\frac{2}{3},\displaystyle\frac{4}{3})\)
以上より領域を図示すると次の通り。
(3)
今度は3つの積です。\(>0\)なので左辺の3つの部分 \(x,y\)\(,x^2+y^2-1\)について、負になるのが0個(3個全部正)か2個(2個負で1個正)として場合分けしても解けますが、\(xy\)を塊としてみて、\(xy\)と\(x^2+y^2-1\)の積として考えると楽です。
\(xy(x^2+y^2-1)\)\(>0\) より
\(xy>0\) かつ \(x^2+y^2-1>0\)・・・①
または
\(xy<0\) かつ \(x^2+y^2-1<0\)・・・②
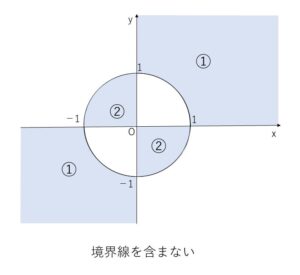
①は \(xy>0\) かつ \(x^2+y^2>1\) (円の外側)
②は \(xy<0\) かつ \(x^2+y^2<1\) (円の内側)
以上より領域を図示すると次の通り。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→正領域・負領域(線分と曲線の共有点) back→不等式の表す領域②(絶対値)