いくつかの\(x,y\)の不等式が与えられたときの、2変数関数の最大最小値を求める問題について見ていきます。
(例題1)
(1)連立不等式
\(x+2y≦4\), \(x-y≦1\), \(x≧0\), \(y≧0\)
の表す領域\(D\)を図示せよ。
(2)点\((x,y)\)が領域\(D\)を動くとき、\(2x+y\)の最大値と最小値を求めよ。
(解答)
(1)
\(x+2y=4\) と \(x-y=1\) の交点を連立して求めると、\((2,1)\)。
また
\(x+2y≦4\) は \(y≦-\displaystyle\frac{1}{2}x+2\)
\(x-y≦1\) は \(y≧x-1\)
以上から領域\(D\)を図示すると次の通り。
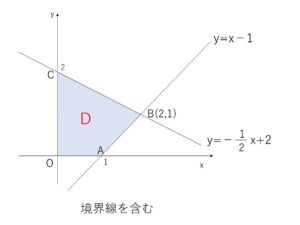
(2)
どう解くかというと、1変数の関数にするために \(2x+y\)\(=k\)とおき、
これを変形すると \(y=-2x+k\)・・・① となり、①は傾き\(-2\),\(y\)切片が\(k\)の直線を表すことがわかります。\(k\)は色々な値をとるので\(k\)を変化させることで直線①は上下に動き色々な直線をとることになります。
では、\(k\)を変化させたときに直線①と\(D\)が共有点をもたない場合はどうなるか考えてみます。
例えば\(k=6\)のときを考えると、\(y=-2x+6\)・・・②となる点、つまり\(2x+y=6(=k)\)となる\((x,y)\)は②上の点ですが、\((x,y)\)は領域\(D\)の中でしか動かないので、\(k=6\)という値はとらないことがわかります。\(k=-1\)も同様です。
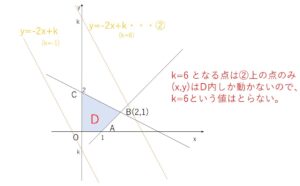
\(k\)が\(D\)と直線①が共有点をもつような値をとるとき、その共有点の\((x,y)\)について\(k\)という値をとるので、\(D\)と直線①が交わるときの\(k\)の最大値最小値を探せばよいことになります。\(k\)は直線①の\(y\)切片なので、\(y\)切片が最大最小となるときを図から判断します。
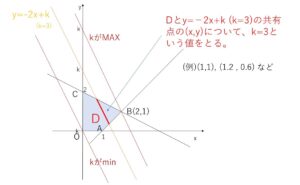
\(2x+y=k\)・・・① とおくと、\(y=-2x+k\)より①は傾き\(-2\),\(y\)切片が\(k\)の直線を表す。
\(D\)と直線①が共有点をもつときを考える。
\(k\)が最大値をとるのは\(k\)が\(y\)切片であることから、①が\(B(2,1)\)を通るとき。このとき共有点は、\((x,y)=(2,1)\)のみで、\(k=2x+y\)\(=2・2+1\)\(=5\)
よって最大値は\(5\)
\(k\)が最小値をとるのは、①が原点\(O\)を通るとき。このとき共有点は \((x,y)=(0,0)\) のみで、\(k=2x+y\)\(=2・0+0\)\(=0\)
よって最小値は\(0\)
線形計画法は利益を最大にするような方法を考えることなどに用いられます。(→(5-9)線形計画法(文章問題)参照)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。