線型計画法(文章問題)

領域と最大最小値に関する文章問題について見ていきます。
文章で書かれたものを数式に変換することがポイントとなります。

(例題)
ある動物は炭水化物とタンパク質については、一定期間にそれぞれ\(700ｇ\)以上,\(400ｇ\)以上摂取しなければならない、と仮定しよう。
2種類の飼料\(A\)と\(B\)があり、それぞれ\(1\)単位に含まれる栄養素の含有量,及び単位あたりの価格が次の表によって与えられている。

(1)各栄養素の最小必要量以上を確保した上で、その総費用を最小にするには、\(A,B\)を何単位(整数単位とする)与えるのがよいか。
(2)\(A\)の単位価格(整数円とは限らない)が上昇したので、総費用を最小にするために\(B\)のみを用いることになった。\(A\)の単位価格は何円を超えたか。

(解答)
(1)

与える\(A,B\)の単位数を\(x,y\)とすると、条件より

\(x+2y≧700\), \(x+y≧400\), \(x≧0\), \(y≧0\)

これらの不等式を満たす\(x,y\)について、総費用 \(11x+12y\)が最小となるときを考える。
\(11x+12y=k\)・・・① とおくと、①は\(y=-\displaystyle\frac{11}{12}x+\displaystyle\frac{k}{12}\)。

不等式の表す領域\(D\)と①が共有点をもつうち\(\displaystyle\frac{k}{12}\)(直線①の\(y\)切片)が最小となるときは図の\(T\)を通るときで、このとき\(k\)も最小。

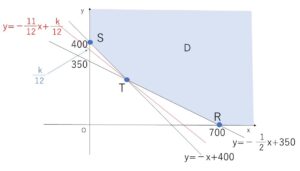
\(x+2y=700\), \(x+y=400\) の交点\(T\)の座標は、\(T(100,300)\)

したがって費用が最小となるのは \(x=100\),\(y=300\) のとき(ともに整数値となる)。

答え \(A\)を\(100\)単位, \(B\)を\(300\)単位

(2)

\(A\)の単位あたりの価格を\(a\)円とすれば、かかる費用は
\(ax+12y=k\)・・・② (\(y=-\displaystyle\frac{a}{12}+\displaystyle\frac{k}{12}\))です。\(x,y\)の条件は(1)のままなので、領域\(D\)と②が共有点をもつときを考えます。\(B\)のみを使用する、つまり\(A\)を全く使わないとき最小費用となるので、②が\(y\)軸上の点を通るとき最小となるときを考えればよく、領域\(D\)の\(y\)軸上の点で\(k\)が最小となるのは\(S(0,400)\)を②が通るときです。
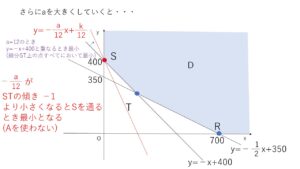
よって、②が\(S\)を通るとき最小となるような\(a\)の条件を求めることになります。(1)の価格設定\(a=11\)では\(T(100,300)\)を通るときが最小となるときで、\(a\)を大きくしていくと直線②の傾きがどんどん小さくなり(傾きが急になり)、しばらくは\(T\)を通るときが最小となるときですが、\(-\displaystyle\frac{a}{12}=-1\) のときには最小となるとき②はぴったり\(y=-x+400\) と重なるので、線分\(ST\)上のすべての座標について、費用が最小となります。これだとまだ\(B\)のみを使ったほうが安いとはいえないので、さらに傾きが小さいとき、つまり\(-\displaystyle\frac{a}{12}<-1\) のとき、\(S\)を通るときに最小となるので、\(a>12\)。よって\(12\)円を超えると\(B\)のみを使用したほうが安くなります。

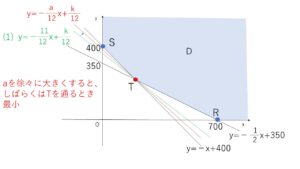
\(A\)の単位あたりの価格を\(a\)円とすれば、かかる費用\(k\)は
\(ax+12y=k\)・・・② (\(y=-\displaystyle\frac{a}{12}+\displaystyle\frac{k}{12}\))

直線②の傾きが直線\(ST\)の傾き\(-1\)より小さいとき、\(k\)が最小となるのは②が\(S(0,400)\) を通るときである。\(x=0\)なので\(A\)を使用しないことになる。

\(-\displaystyle\frac{a}{12}<-1\) を解くと
\(a>12\)

したがって12円を超えると\(B\)のみを使用した(\(A\)を使用しない)ほうが費用が最小となる。

答 \(12\)円

以上になります。御疲れ様でした。
ここまで見て頂きありがとうございました。

next→命題と領域　back→領域と最大・最小値③(分数式・変換)