三角関数を含む不等式で表された領域の問題について見ていきます。
(例題)
\(xy\)平面において、連立不等式
\(0≦x≦π\), \(0≦y≦π\)
\(2\sin(x+y)-2\cos(x+y)≧\sqrt{2}\)
の表す領域を\(D\)とする。このとき以下の問いに答えよ。
(1)\(D\)を図示せよ。
(2)点\((x,y)\)が領域\(D\)を動くとき、\(2x+y\) の最大値と最小値を求めよ。
(解答)
(1)
\(2\sin(x+y)-2\cos(x+y)≧\sqrt{2}\) より
\(2\sqrt{2}\sin(x+y-\displaystyle\frac{π}{4})≧\sqrt{2}\)
\(\sin(x+y-\displaystyle\frac{π}{4})≧\displaystyle\frac{1}{2}\)・・・①
\(0≦x≦π\), \(0≦y≦π\) より
\(-\displaystyle\frac{π}{4}≦x+y-\displaystyle\frac{π}{4}≦\displaystyle\frac{7π}{4}\) だから
①より
\(\displaystyle\frac{π}{6}≦x+y-\displaystyle\frac{π}{4}≦\displaystyle\frac{5π}{6}\)
よって
\(\displaystyle\frac{5π}{12}≦x+y≦\displaystyle\frac{13π}{12}\)・・・②
②と \(0≦x≦π\), \(0≦y≦π\) を図示すると
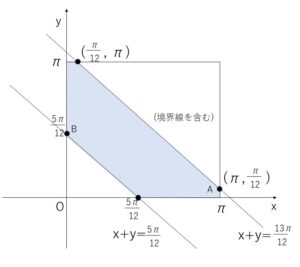
(2)
(1)で領域\(D\)を図示したので、\(2x+y=k\)・・・③ とおいて、直線③と領域\(D\)が共有点をもつときの\(k\)の最大値と最小値を考えます。(線形計画法)
③の傾きは\(-2\)で、境界線の傾き\(-1\)より小さい(傾きとしては急)なので、図の点\(A,B\)を③が通るときにそれぞれ最大,最小値となります。
\(2x+y=k\)・・・③ とおく
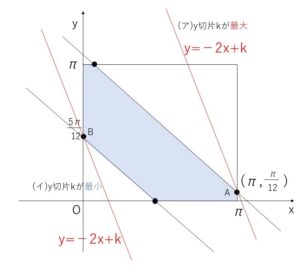
\(y=-2x+k\) (傾き\(-2\))が領域\(D\)と共有点をもつとき、\(y\)切片\(k\)が
(ア)
最大となるときは、\(A(π,\displaystyle\frac{π}{12})\) を③が通るときなので
最大値 \(k=2π+\displaystyle\frac{π}{12}\)\(=\displaystyle\frac{25π}{12}\)
(イ)
最小となるときは、\(B(0,\displaystyle\frac{5π}{12})\) を③が通るときなので
最小値 \(k=2\cdot0+\displaystyle\frac{5π}{12}\)\(=\displaystyle\frac{5π}{12}\)
(答)
最大値 \(\displaystyle\frac{25π}{12}\) (\(x,y)=(π,\displaystyle\frac{π}{12})\)
最小値 \(\displaystyle\frac{5π}{12}\) (\(x,y)=(0,\displaystyle\frac{5π}{12})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→0や負の整数の指数 back→三角関数の図形への応用