指数法則や累乗根の性質を利用して、計算問題を解いていきます。
累乗根の性質と指数法則を念のため載せておきます。
\(a>0\), \(b>0\) かつ \(m,n,p\)が正の整数のとき
①\(\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}\) (同じ\(n\)乗根はまとめられる)
②\(\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\displaystyle\frac{a}{b}}\) (同じ\(n\)乗根はまとめられる)
③\((\sqrt[n]{a})^m=\sqrt[n]{a^m}\)
④\(\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}\)
⑤\(\sqrt[n]{a^m}=\sqrt[np]{a^{mp}}\) (\(p\)乗したら\(p\)乗根とって帳尻あわせ)
\(a>0\), \(b>0\) で、\(r,s\)が実数のとき
①\(a^ra^s=a^{r+s}\) ①’ \(a^r÷a^s=a^{r-s}\)
②\((a^r)^s=a^{rs}\)
③\((ab)^r=a^rb^r\) ③’ \((\displaystyle\frac{a}{b})^r=\displaystyle\frac{a^r}{b^r}\)
基本的には、累乗根をすべて有理数の指数に直して、指数法則のみを適用していきます。
累乗根の有理数の指数への変換は
\(\sqrt[n]{a^m}=a^{\frac{m}{n}}\)
です。
(例題)次の計算をせよ。
(1)\(\sqrt[3]{2^4}×2^{-\frac{1}{2}}×\sqrt[6]{2^7}\)
(2)\(\sqrt{3}×\sqrt[4]{6}×\displaystyle\frac{1}{\sqrt[4]{540}}×\sqrt[4]{10}\)
(3)\((6^{\frac{2}{3}}+6^{-\frac{2}{3}}+1)(6^{\frac{1}{3}}-6^{-\frac{1}{3}})\)
(4)\(\sqrt[3]{24}+\displaystyle\frac{4}{3}\sqrt[6]{9}+\sqrt[3]{-\displaystyle\frac{1}{9}}\)
(解答)
(1)
(すべて累乗の形に直すと)
\(\sqrt[3]{2^4}×2^{-\frac{1}{2}}×\sqrt[6]{2^7}\)
\(=2^{\frac{4}{3}}×2^{-\frac{1}{2}}×2^{\frac{7}{6}}\)
\(=2^{\frac{4}{3}-\frac{1}{2}+\frac{7}{6}}\)
\(=2^{2}\)
\(=4\)
(2)
(解1 累乗の形にすると)
\(\sqrt{3}×\sqrt[4]{6}×\displaystyle\frac{1}{\sqrt[4]{540}}×\sqrt[4]{10}\)
\(=3^{\frac{1}{2}}×(2\cdot3)^{\frac{1}{4}}×(2^2\cdot3^3\cdot5)^{-\frac{1}{4}}×(2\cdot5)^{\frac{1}{4}}\)
(2,3,5の累乗で整理して)
\(=2^{\frac{1}{4}-\frac{2}{4}+\frac{1}{4}}×3^{\frac{1}{2}+\frac{1}{4}-\frac{3}{4}}×5^{-\frac{1}{4}+\frac{1}{4}}\)
\(=2^0×3^0×5^0\)
\(=1\)
(解2 4乗根で統一すると)
\(\sqrt{3}×\sqrt[4]{6}×\displaystyle\frac{1}{\sqrt[4]{540}}×\sqrt[4]{10}\)
\(=\sqrt[4]{3^2}×\sqrt[4]{6}×\displaystyle\frac{1}{\sqrt[4]{540}}×\sqrt[4]{10}\)
\(=\sqrt[4]{\displaystyle\frac{3^2\cdot6\cdot10}{540}}\)
\(=\sqrt[4]{1}\)
\(=1\)
(3)
\((x-y)(x^2+xy+y^2)=x^3-y^3\)
を意識すると、\(6^{\frac{1}{3}}×6^{-\frac{1}{3}}=6^{\frac{1}{3}-\frac{1}{3}}=1\) (逆数の積になっている)
より、この公式が適用できる形になっています。
\((6^{\frac{2}{3}}+6^{-\frac{2}{3}}+1)(6^{\frac{1}{3}}-6^{-\frac{1}{3}})\)
\(=(6^{\frac{2}{3}}+6^{\frac{1}{3}}\cdot6^{-\frac{1}{3}}+6^{-\frac{2}{3}})(6^{\frac{1}{3}}-6^{-\frac{1}{3}})\)
\(=(6^{\frac{1}{3}})^3-(6^{-\frac{1}{3}})^3\)
\(=6^1-6^{-1}\)
\(=6-\displaystyle\frac{1}{6}\)
\(=\displaystyle\frac{35}{6}\)
(4)
まず根号の中身が負でよいのかという点ですが、3乗根(奇数乗根)なので、3乗して負になる実数は全然あるので問題ないです。
次に中身が負の根号の取り扱いですが、
\(\sqrt[n]{-a}=-\sqrt[n]{a}\)
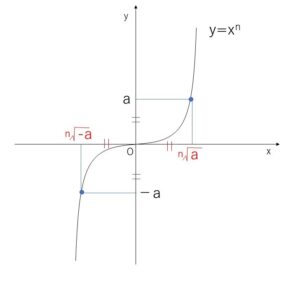
と符号を外に出すことになります。なぜこの等式が成り立つかというと、\(y=x^n\) (\(n\)は奇数) のグラフは原点対称で、2点 \((\sqrt[n]{a},a)\) と \((\sqrt[n]{-a},-a)\) は\(y\)座標の絶対値が同じなのでちょうど対称な点だから、\(x\)座標の絶対値も同じなので、\(\sqrt[n]{a}=-\sqrt[n]{-a}\) となるからです。
(解1 累乗の形にすると)
\(\sqrt[3]{24}+\displaystyle\frac{4}{3}\sqrt[6]{9}+\sqrt[3]{-\displaystyle\frac{1}{9}}\)
\(=(2^3\cdot3)^{\frac{1}{3}}+\displaystyle\frac{4}{3}\cdot(3^2)^{\frac{1}{6}}-\sqrt[3]{\displaystyle\frac{1}{9}}\)
\(=2\cdot3^{\frac{1}{3}}+\displaystyle\frac{4}{3}\cdot3^{\frac{1}{3}}-3^{-\frac{2}{3}}\)
\(3^{-\frac{2}{3}}=3^{-1+\frac{1}{3}}=3^{-1}3^{\frac{1}{3}}\)
です。あとは\(3^{\frac{1}{3}}\) を文字のようにみて係数を計算します。
\(=2\cdot3^{\frac{1}{3}}+\displaystyle\frac{4}{3}\cdot3^{\frac{1}{3}}-3^{-1}3^{\frac{1}{3}}\)
\(=(2+\displaystyle\frac{4}{3}-3^{-1})\cdot3^{\frac{1}{3}}\)
\(=(2+\displaystyle\frac{4}{3}-\displaystyle\frac{1}{3})\cdot3^{\frac{1}{3}}\)
\(=3\cdot3^{\frac{1}{3}}\) (←これを答えにしてもよい)
\(=3\sqrt[3]{3}\)
(解2 根号のままで解くと)
まずは3乗根で統一、素因数分解して中身を小さくすると
\(\sqrt[3]{24}+\displaystyle\frac{4}{3}\sqrt[6]{9}+\sqrt[3]{-\displaystyle\frac{1}{9}}\)
\(=\sqrt[3]{2^3\cdot3}+\displaystyle\frac{4}{3}\sqrt[6]{3^2}-\sqrt[3]{\displaystyle\frac{1}{3^2}}\)
2項目は、累乗根の性質⑤より、6乗根の「6」と中身の2乗の「2」を両方2で割ります。
3項目は、分母の有理化を行うため、分母分子に3をかけます。
\(=\sqrt[3]{2^3}\cdot\sqrt[3]{3}+\displaystyle\frac{4}{3}\sqrt[3]{3}-\sqrt[3]{\displaystyle\frac{3}{3^3}}\)
\(=2\sqrt[3]{3}+\displaystyle\frac{4}{3}\sqrt[3]{3}-\displaystyle\frac{\sqrt[3]{3}}{3}\)
(すべて\(\sqrt[3]{3}\)に統一できたので、あとは係数を計算するだけです)
\(=(2+\displaystyle\frac{4}{3}-\displaystyle\frac{1}{3})\sqrt[3]{3}\)
\(=3\sqrt[3]{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→指数の計算② back→累乗根、有理数・無理数の指数