・接線の方程式
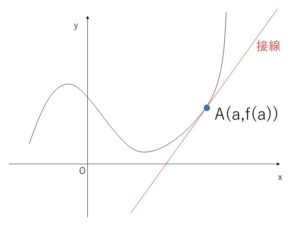
関数 \(y=f(x)\) 上の 点\(A(a,f(a))\) における微分係数 \(f'(a)\) は、点\(A\)における接線の傾きを表していました。
点\(A\)における接線は、「傾き\(f'(a)\)で \((a,f(a))\) を通る直線」なので、その方程式は
\(y-f(a)=f'(a)(x-a)\)
(例題1)
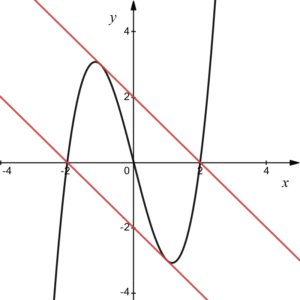
関数 \(y=x^3-4x\)・・・① において
(1) ①上の点\((1,-3)\) における接線の方程式を求めよ。
(2) 傾きが\(-1\)である接線の方程式を求めよ。
(解答)
(1)
\(y’=3x^2-4\) より
\((1,-3)\)における微分係数は
\(y’=3-4=-1\)
よって接線の方程式は
\(y+3=-1(x-1)\)
\(y=-x-2\)
(2)
微分係数が \(-1\) だから
\(3x^2-4=-1\)
\(x^2=1\)
\(x=±1\) (接点の\(x\)座標)
\(x=1\) のとき \(y=1-4=-3\)
\(x=-1\) のとき \(y=-1+4=3\)
よって、\((1,-3)\) と \((-1,3)\) における接線の方程式を求めればよい。
\((1,-3)\) における接線の方程式は(1)より
\(y=-x-2\)
\((-1,3)\) における接線の方程式は
\(y-3=-(x+1)\)
\(y=-x+2\)
(例題2)
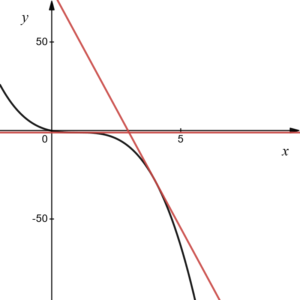
曲線 \(y=-x^3+3x^2-3x\) について、点\((3,-1)\) を通る接線の方程式を求めよ。
(解答)
\(y’=-3x^2+6x-3\)
接点を \((t,-t^3+3t^2-3t)\) とおくと、接線の方程式は
\(y-(-t^3+3t^2-3t)=(-3t^2+6t-3)(x-t)\)・・・①
①が\((3,-1)\) を通るので
\(-1-(-t^3+3t^2-3t)=(-3t^2+6t-3)(3-t)\)
整理して
\(t^3-6t^2+9t-4=0\)
\((t-1)^2(t-4)=0\)
よって
\(t=1,4\)
したがって①より接線の方程式は
\(t=1\) のとき
\(y+1=0\)
\(y=-1\)
\(t=4\) のとき
\(y+28=-27(x-4)\)
\(y=-27x+80\)
(例題3)
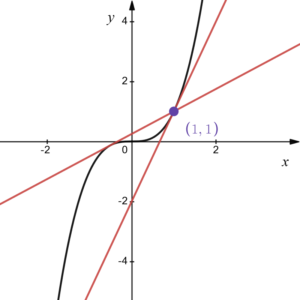
曲線 \(y=x^3\) 上の点\((1,1)\)を通る接線を求めよ。
この問題も例題2と同様に接点を\((t,f(t))\)とおきます。(曲線の外部にあるか曲線上にあるかの違いだけなので、本質的には同じ)
(解答)
\(y’=3x^2\)
接点を \((t,t^3)\) とおくと、接線の方程式は
\(y-t^3=3t^2(x-t)\)・・・①
①が \((1,1)\) を通るので
\(1-t^3=3t^2(1-t)\)
整理して
\(2t^3-3t^2+1=0\)
\((t-1)^2(2t+1)=0\)
\(t=1,-\displaystyle\frac{1}{2}\)
①より、接線の方程式は
\(t=1\) のとき
\(y-1=3(x-1)\)
\(y=3x-2\)
\(t=-\displaystyle\frac{1}{2}\) のとき
\(y+\displaystyle\frac{1}{8}=\displaystyle\frac{3}{4}(x+\displaystyle\frac{1}{2})\)
\(y=\displaystyle\frac{3}{4}x+\displaystyle\frac{1}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線の基礎② back→関数の決定・関数方程式