接線の基礎②

前回の知識をもとに色々な接線に関する演習問題を解いていきます。

(例題1)
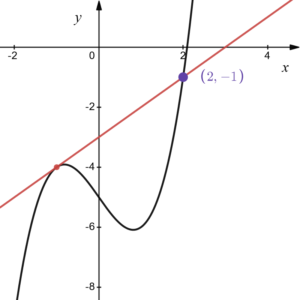
曲線 \(y=x^3-2x-5\) を\(C\)とする。点\((3,0)\) から曲線\(C\)へは複数の接線が引けるが、それらのうち傾きの値が最も小さい接線を\(l\)とする。

(1)\(l\)の方程式を求めよ。
(2)曲線\(C\)と接線\(l\)が、接点以外に共有する点の座標を求めよ。

(解答)

(1)
\(y’=3x^2-2\)

接点を \((t,t^3-2t-5)\) とおくと、接線の方程式は
\(y-(t^3-2t-5)=(3t^2-2)(x-t)\)

整理して
\(y=(3t^2-2)x-2t^3-5\)・・・①

①が \((3,0)\) を通るので
\(0=(3t^2-2)\cdot3-2t^3-5\)
\(2t^3-9t^2+11=0\)
\((t+1)(2t^2-11t+11)=0\)

\(t=-1,\displaystyle\frac{11±\sqrt{33}}{4}\)

ここで

\(\displaystyle\frac{11+\sqrt{33}}{4}>\displaystyle\frac{11-\sqrt{33}}{4}>\displaystyle\frac{11-6}{4}=1.25>1\)

だから、傾き \(y’=3t^2-2\) が最小となるのは、絶対値が最も小さい \(t=-1\)

したがって①より接線\(l\)の方程式は
\(y=x-3\)

(2)

\(y=x-3\)・・・②
\(y=x^3-2x-5\)・・・③

②,③より
\(x-3=x^3-2x-5\)
\(x^3-3x-2=0\)・・・④

\((x+1)^2(x-2)=0\)

よって、接点以外の共有点の\(x\)座標は \(x=2\)
②より \(y=-1\)

したがって座標は
\((2,-1)\)

(例題2)
放物線 \(y=x^2+ax+b\) が 点\((2,2)\) を通り、かつ 直線 \(y=2x-2\) に接するように \(a,b\) の値を求めよ。また、そのときの接点の座標を求めよ。

(解答)
\(y=x^2+ax+b\) において \((2,2)\) を通るから

\(2=4+2a+b\)・・・①

\(y’=2x+a\) より、接点を \((t,t^2+at+b)\) とおくと、接線の方程式は

\(y-(t^2+at+b)=(2t+a)(x-t)\)
整理して
\(y=(2t+a)x-t^2+b\)・・・②

②が \(y=2x-2\) となるから
\(2t+a=2\)・・・③
\(-t^2+b=-2\)・・・④

①より \(b=-2a-2\)
④に代入して
\(t^2+2a=0\)・・・⑤
⑤に③を代入して
\(t^2-4t+4=0\)
\((t-2)^2=0\)
\(t=2\)

③④より
\(a=-2\),　\(b=2\)

また接点の座標は \((t,t^2+at+b)\) より
\((2,2)\)

(例題3)
放物線 \(y=x^2\) の動点を\(P\)とする。\(P\)におけるこの放物線の接線と\(y\)軸の交点を\(Q\)とする。\(P\)が原点と異なるとき、線分\(PQ\)の垂直二等分線は常に\(y\)軸上の定点を通ることを証明せよ。

(解答)

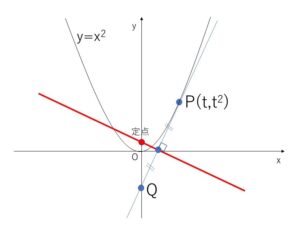
\(P(t,t^2)\) \((t≠0)\)とおく。

\(y’=2x\) より 点\(P\)における接線の方程式は
\(y=2t(x-t)+t^2\)・・・①

①で \(x=0\) とすると
\(y=-t^2\) だから
\(Q(0,-t^2)\)

\(P,Q\)の中点は \((\displaystyle\frac{t}{2},0)\) で
垂直二等分線の傾きは①に垂直であるから、\(-\displaystyle\frac{1}{2t}\)

よって垂直二等分線の方程式は
\(y=-\displaystyle\frac{1}{2t}(x-\displaystyle\frac{t}{2})\)・・・②

②を\(t\)について整理すると
\(\displaystyle\frac{1}{2t}x+(y-\displaystyle\frac{1}{4})=0\)・・・③

\(x=0\), \(y=\displaystyle\frac{1}{4}\) のとき、③は\(t\)によらず成り立つ。

したがって垂直二等分線は\(t\)の値によらず、\(y\)軸上の定点 \((0,\displaystyle\frac{1}{4})\) を通る。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→共通接線①(2曲線が接する)　back→接線の基礎①