関数に文字を含む、最大最小値に関する問題について見ていきます。
(例題)
定数\(a\)に対して
関数 \(f(x)=x^3-3a^2x\)
の \(-1≦x≦1\) における最大値を\(M(a)\)とする。\(a\)が実数全体を動くとき
(1)\(M(a)\)を\(a\)を用いて表せ。
(2)\(M(a)\)の最小値を求めよ。
もちろん微分してグラフの増減を調べますが、\(a\)の値によって極値が区間内にあったりなかったり、極大と極小のときの\(x\)の値が変わったりするので場合分けします。
(解答)
(1)
\(f(x)=x^3-3a^2x\) \(-1≦x≦1\) において
\(f'(x)=3(x+a)(x-a)\)
\(f'(x)=0\) となるのは \(x=±a\)
①\(a=0\), ②\(a>0\), ③\(a<0\) で場合分けします。
また、区間が \(-1≦x≦1\) なので、極値(極大値)が区間にあるかどうかで ②③をさらに
②-A \(0<a<1\) ②-B \(a≧1\)
③-A \(-1<a<0\) ③-B \(a≦-1\)
で場合分けします。
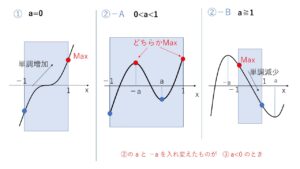
① \(a=0\) のとき
\(f'(x)=3x^2≧0\) より
\(f(x)\) は単調増加になる。よって最大値は
\(M(a)=f(1)=1\)
②-A \(0<a<1\) のとき
\(-a<a\) より増減表は次の通り
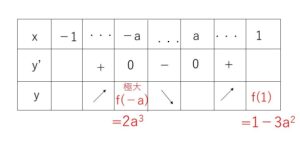
\(f(-a)-f(1)=2a^3+3a^2-1\)
\(=(a+1)^2(2a-1)\) より
\(0<a≦\displaystyle\frac{1}{2}\) のとき
\(f(-a)≦f(1)\) だから
\(M(a)=f(1)=1-3a^2\)
\(\displaystyle\frac{1}{2}<a<1\) のとき
\(f(-a)>f(1)\) だから
\(M(a)=f(-a)=2a^3\)
②-B \(a≧1\) のとき
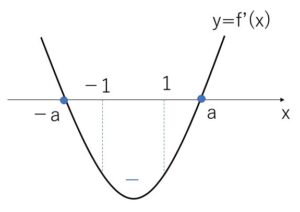
\(f'(x)=3(x+a)(x-a)\) は
\(-1≦x≦1\) の範囲で \(f'(x)≦0\)
したがって\(f(x)\)は単調減少になるから
\(M(a)=f(-1)=-1+3a^2\)
\(-a>a\) となり、②-A,B の \(-a\) と \(a\) がただ入れ替わっただけなので、これらを利用します。
③ \(a<0\) のとき
②-A,B について 「\(a→-a\)」、「 \(-a→a\)」 と置き換えればよいので
\(0<-a≦\displaystyle\frac{1}{2}\) のとき
つまり、\(-\displaystyle\frac{1}{2}≦a<0\) のとき
\(M(a)=f(1)=1-3a^2\)
\(\displaystyle\frac{1}{2}<-a<1\) のとき
つまり、\(-1<a<-\displaystyle\frac{1}{2}\) のとき
\(M(a)=\)\(f(a)=-2a^3\)
\(-a≧1\)のとき
つまり、\(a≦-1\) のとき
\(M(a)=f(-1)=-1+3a^2\)
\(a=0\) を \(M(a)=f(1)=1-3a^2\) に含めて
以上をまとめると
\(\begin{eqnarray} \color {red} {M(a) =} \begin{cases} \color{red}{-1+3a^2} & (a≦-1,\ a≧1)
\\ \color{red}{-2a^3} & (-1<a<-\frac{1}{2})
\\ \color{red}{1-3a^2} & (-\frac{1}{2} ≦a≦\frac{1}{2} )
\\ \color{red}{2a^3} & (\frac{1}{2}<a<1)
\end{cases} \end{eqnarray}\)
(2)
(1)より \(M(a)\) のグラフを書くと次の通り。
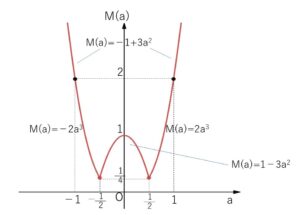
したがって、\(M(a)\)の最小値は
\(\displaystyle\frac{1}{4}\) (\(a=±\displaystyle\frac{1}{2}\))
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→最大・最小値②(文字含む) back→最大・最小値の基礎