引き続き、不等式に関する問題について見ていきます。
(例題1)
2つの関数
\(f(x)=-x^4+x^2+2x+5\)
\(g(x)=4x^2+12x+a\) (ただし\(a\)は実数で定数とする)
について次の問いに答えよ。
(1)どのような実数\(x\)に対しても \(f(x)<g(x)\) となる\(a\)の値の範囲を求めよ。
(2)どのような実数\(x_1,x_2\)に対しても \(f(x_1)<g(x_2)\) となる\(a\)の値の範囲を求めよ。
例えば次の図では、(1)の条件は満たしていますが(2)の条件は満たしていません。
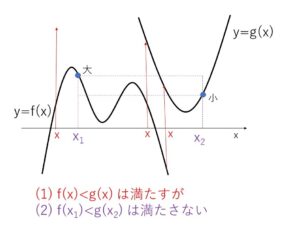
(解答)
(1)
\(h(x)=g(x)-f(x)\) とおいて、実数全体の\(x\)について \(h(x)>0\) となる\(a\)の値の範囲を求めればよい。
\(h(x)=x^4+3x^2+10x+a-5\)
\(h'(x)=2(2x^3+3x+5)\)\(=2(x+1)(2x^2-2x+5)\)
\(2x^2-2x+5=0\) の判別式は負の値なので、\(2x^2-2x+5>0\)
よって増減表は次の通り。

したがって、\(h(x)>0\)となるためには
\(h(-1)>0\)
\(a-11>0\)
\(a>11\)
(2)
(\(f(x)\) の最大値)<(\(g(x)\)の最小値) となる\(a\)の範囲を求めることになります。
図示して考えると、2つの曲線の間に\(x\)軸に平行な直線が引けるイメージです。
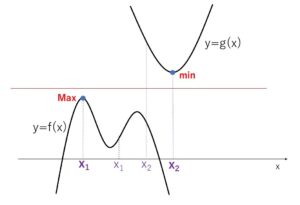
題意を満たすには
(\(f(x)\) の最大値)<(\(g(x)\)の最小値) となる\(a\)の値の範囲を求めればよい。
\(f(x)=-x^4+x^2+2x+5\) より
\(f'(x)=-2(2x^3-x-1)=-2(x-1)(2x^2+2x+1)\)
\(2x^2+2x+1=0\) の判別式は負の値になるので、\(2x^2+2x+1>0\)
よって増減表は次の通り。

\(f(x)\)の最大値は
\(f(1)=7\)
\(g(x)=4x^2+12x+a=4(x+\displaystyle\frac{3}{2})^2-9+a\) より
\(g(x)\)の最小値は \(a-9\)
したがって
\(7<a-9\) より
\(a>16\)
((2)のほうがより厳しい条件となっています)
(例題2)
\(s\)を実数、\(t\)を\(0\)以上の実数とし、関数\(f(x)\)を
\(f(x)=x^3-sx^2+(t-2s^2)x+st\)
により定める。関数 \(f(x)\) に対して次の条件\(p\)を考える。
\(p:\) \(0≦x≦1\)を満たすすべての\(x\)に対して \(f(x)>0\) である。
このとき、条件\(p\)を満たす点\((s,t)\)の領域を図示せよ。
そこで着目してほしいのが \(f(x)=0\) の解の1つが \(x=-s\) であることです。
次数の高い関数では、まず最初に \(f(x)=0\) の解、つまり\(x\)軸との交点の座標を求めることができるかどうか確認することも大事です。
また間の数はともかく、少なくとも端点の \(f(0),f(1)\) の両方がどちらも正の数でなくてはならないことにも着目します(必要条件として出てくる)。(この問題では \(f(1)>0\) は使いません)
(解答)
\(f(x)=x^3-sx^2+(t-2s^2)x+st\)
\(=(x+s)(x^2-2sx+t)\)
条件を満たすには \(f(0)>0\) だから
\(st>0\)
\(t≧0\) より \(s>0\)
よって、\(0≦x≦1\)の範囲では \(x+s>0\)
ただの2次関数の問題です。
\(g(x)=x^2-2sx+t\)
\(=(x-s)^2-s^2+t\) とおくと
2次関数 \(y=g(x)\) が \(0≦x≦1\) の範囲で \(g(x)>0\) となる条件を求めればよい。
軸 \(x=s\) が範囲内にあるかどうかで場合分けして
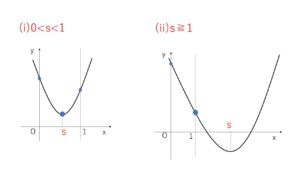
(i)\(0<s<1\) のとき
\(y=g(x)\) の最小値は \(g(s)=-s^2+t\) だから
\(-s^2+t>0\)
(ii)\(s≧1\) のとき
\(y=g(x)\) の最小値は \(g(1)=1-2s+t\) だから
\(1-2s+t>0\)
まとめると
「\(0<s<1\) かつ \(t>s^2\)」
または
「\(s≧1\) かつ \(t>2s-1\)」
図示すると次の通り。
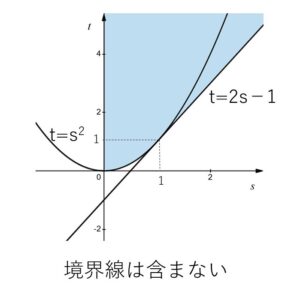
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→高次方程式の実数解のとりうる範囲 back→不等式と微分①