微分を利用する、不等式の証明・成立条件に関する問題について見ていきます。
(例題1)
\(x≧-4\) のとき \(x^3-7>12(x-2)\) が成り立つことを証明せよ。
よって、この関数を微分して増減を調べ、\(x≧-4\) の範囲で正になることを示せればOKです。
(左辺)-(右辺)
\(=x^3-12x+17\)
(\(=f(x)\) とおく)
\(f'(x)=3(x+2)(x-2)\) より \(x≧-4\) での増減表は次の通り。
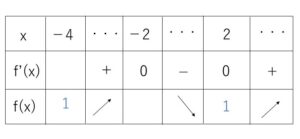
よって最小値は\(1\)だから
\(f(x)>0\)
したがって与えられた不等式は成り立つ。
(例題2)
\(a\)を実数とし、関数 \(f(x)=x^3-3ax+a\) を考える。\(0≦x≦1\) において \(f(x)≧0\) となるような\(a\)の範囲を求めよ。
(解答)
\(f'(x)=3(x^2-a)\)
(ア)\(a≦0\) のとき
\(f'(x)≧0\) より \(y=f(x)\)は単調増加。
よって最小値が \(f(0)=a\) だから、\(f(x)≧0\) になるためには
\(a≧0\)
\(a≦0\) だから条件を満たすのは
\(a=0\)
(イ)\(a>0\) のとき
\(f'(x)=0\) を満たすのは
\(x=±\sqrt{a}\)
極値をとる\(x\)が範囲内にあるかどうか、つまり
(i)\(0<a<1\), (ii)\(a≧1\) で場合分けすると増減表は次の通り。

(i)\(0<a<1\) のとき
\(f(x)≧0\) となるためには
\(f(\sqrt{a})≧0\)
\(-2a\sqrt{a}+a≧0\)
\(a(-2\sqrt{a}+1)≧0\)
\(a>0\) より
\(-2\sqrt{a}+1≧0\)
\(\sqrt{a}≦\displaystyle\frac{1}{2}\)
よって、\(0<a<1\) と合わせると
\(0<a≦\displaystyle\frac{1}{4}\)
(ii)\(a≧1\) のとき
\(f(x)≧0\) となるためには
\(f(1)≧0\)
\(1-2a≧0\)
\(a≦\displaystyle\frac{1}{2}\)
\(a≧1\) を満たさないので不適。
以上から
\(0≦a≦\displaystyle\frac{1}{4}\)
(例題3)
\(x>0\) の範囲で、曲線 \(y=ax^3+b\) が放物線 \(y=x^2\) より上方にあるための、\(a,b\)の条件を求めよ。
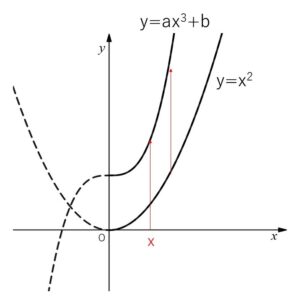
(解答)
\(h(x)=ax^3+b-x^2\) とおくと、条件を満たすには
\(x>0\) の範囲で \(h(x)>0\) になればよい。
(ア)\(a=0\) のとき
\(h(x)=b-x^2\) より、単調減少関数だから \(h(x)>0\) にならず不適。
(イ)\(a≠0\) のとき
\(h'(x)=3ax(x-\displaystyle\frac{2}{3a})\)
(i)\(a<0\) のとき
\(x>0\) の範囲で \(x(x-\displaystyle\frac{2}{3a})>0\) だから
\(h'(x)<0\) となり単調減少関数だから、\(h(x)>0\) にならず不適。
(ii)\(a>0\) のとき
増減表は次の通り。
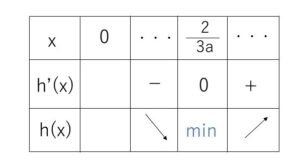
よって、\(h(x)>0\) になるためには
\(h(\displaystyle\frac{2}{3a})>0\)
\(-\displaystyle\frac{4}{27a^2}+b>0\)
\(b>\displaystyle\frac{4}{27a^2}\)
したがって
\(a>0\) かつ \(b>\displaystyle\frac{4}{27a^2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→不等式と微分② back→接線の本数②