今まで軌跡や領域を図示する例題を扱うこともありましたが、今回からは特に軌跡・領域の要素が強いものについて扱っていきます。
(例題1)
放物線 \(C:y=x^2\) 上の点\(P\)を通り、かつ\(P\)における\(C\)の接線に垂直な直線を\(l_1\)とする。同様に、\(C\)上の点\(Q\)を通り、かつ\(Q\)における\(C\)の接線に垂直な直線を\(l_2\)とする。\(l_1\)と\(l_2\)が直交するとき、\(l_1\)と\(l_2\)の交点\(R\)の軌跡を求めよ。
(解答)
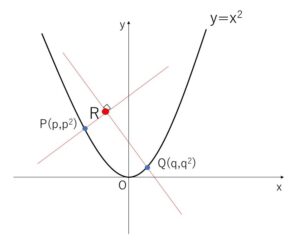
\(P(p,p^2)\), \(Q(q,q^2)\) とおく。
\(l_1,l_2\) が直交するので、\(p≠q\)
また、原点における法線は\(x\)軸に垂直で条件を満たさないので、\(p≠0\), \(q≠0\)
\(C\)について \(y’=2x\) より
\(l_1:y=-\displaystyle\frac{1}{2p}(x-p)+p^2\)
\(l_2:y=-\displaystyle\frac{1}{2q}(x-q)+q^2\)
整理して
\(l_1:y=-\displaystyle\frac{1}{2p}x+p^2+\displaystyle\frac{1}{2}\)・・・①
\(l_2:y=-\displaystyle\frac{1}{2q}x+q^2+\displaystyle\frac{1}{2}\)・・・②
\(l_1,l_2\) が直交するから
\((-\displaystyle\frac{1}{2p})(-\displaystyle\frac{1}{2q})=-1\)
よって
\(pq=-\displaystyle\frac{1}{4}\)・・・③
①②より \(R(x,y)\) の座標を求めると
①-② から
\((\displaystyle\frac{1}{2q}-\displaystyle\frac{1}{2p})x=q^2-p^2\)
\(\displaystyle\frac{p-q}{2pq}x=-(p-q)(p+q)\)
\(p≠q\), ③ より
\(p+q=2x\)・・・④
①+②より
\(2y=-(\displaystyle\frac{1}{2p}+\displaystyle\frac{1}{2q})x+p^2+q^2+1\)
\(2y=-\displaystyle\frac{p+q}{2pq}x+(p+q)^2-2pq+1\)
③④より
\(y=4x^2+\displaystyle\frac{3}{4}\)
\(pq=-\displaystyle\frac{1}{4}\)・・・③
\(p+q=2x\)・・・④
に着目すると和と積の形になっているため、\(x,y\)が実数であっても\(p,q\)が実数であり、さらに互いに異なる保証がありません。したがって、\(p,q\)が異なる実数であることを確認する必要があります。(\(0\)でないことは③から分かりますがそれも断っておきます)
ここで③④より \(p,q\)は\(t\)の2次方程式
\(t^2-2xt-\displaystyle\frac{1}{4}=0\)
の\(0\)でない異なる2つの実数解である。
よって、\(D>0\) であるが
\(\displaystyle\frac{D}{4}=x^2+\displaystyle\frac{1}{4}>0\) はすべての実数\(x\)で成り立ち、また③より\(p,q\)は\(0\)でない。
したがって求める軌跡は
放物線 \(y=4x^2+\displaystyle\frac{3}{4}\)
(例題2)
\(y=x^3+3t^2x+t^3\)・・・① とする。
(1)①の右辺を\(t\)の関数とみなして\(f(t)\)とおく。\(x\)が正の数の場合、関数\(f(t)\)の極値を求めよ。
(2)\(t\)が\(t>0\)の範囲で変化するとき、\(x\)の3次関数①のグラフが通過する領域を\(xy\)平面上に図示せよ。
(解答)
(1)
①を\(t\)について整理して
\(f(t)=t^3+3xt^2+x^3\)
\(f'(t)=3t(t+2x)\)
\(f'(t)=0\) のとき \(t=0,-2x\) であり、\(x>0\) より \(-2x<0\) となるから増減表は次の通り。
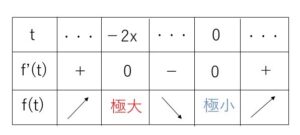
したがって
極大値 \(f(-2x)=5x^3\)
極小値 \(f(0)=x^3\)
(2)
領域を考える問題は大きく分けて、(i)順像法 (ii)逆像法 の2パターンがありますが、この例題はどちらの方法でも解くことができます。それぞれの解法で解いていきます。
(解答 i) 順像法
\(y=t^3+3xt^2+x^3\)・・・①
について例えば \(x=1\) のときの \(y\)がどうなるかを考えると
\(y=t^3+3t^2+1\) とただの\(t\)の3次関数になるので、\(y\)の範囲は簡単に求まります。他の\(x\)についても同様に\(t\)の関数になるのでそれらを網羅的に考えたものが求める範囲になりますが、すべての\(x\)について具体的に考えるわけにはいかないので、\(x=k\) (\(k\)は文字定数) とおいて(①は\(x,t\)の2変数なので、一方の\(x\)を固定するという)、文字定数\(k\)を含む\(t\)の3次関数として\(y\)の範囲を考えます。
\(y=2x\) などの\(x\)以外の文字が無い場合のグラフは\(x\)を1つ決めると\(y\)が1決まる(つまり点になる)のですが、①は\(t\)があるので\(x\)1つについて\(y\)がいくつか存在する(線上になる)ことになり、\(x\)全部をあわせると領域になるわけです。
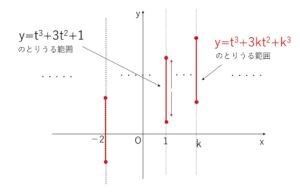
\(x=k\) として固定すると
\(f(t)=t^3+3kt^2+k^3\)
\(f'(t)=3t(t+2k)\)
\(f'(t)=0\) となるのは \(t=0,-2k\)
したがって、\(k\)の正負によって\(f(t)\)のグラフの増減(形状)が異なるので場合分けします。なお\(k>0\) については、\(t>0\)の制約以外は(1)と同様の増減表になります。
(ア) \(k=0\) のとき
\(f'(t)=3t^2>0\) より単調増加だから
\(y=f(t)>f(0)=k^3=0\)
よって
\(y>0\)
(イ) \(k≠0\) のとき
\(k<0\), \(k>0\) のときの増減表は次の通り。
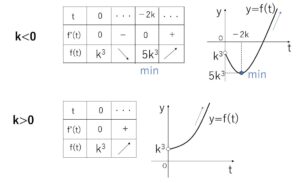
よって \(y=f(t)\)の範囲は
\(k<0\) のとき \(y≧5k^3\)
\(k>0\) のとき \(y>k^3\)
これで\(y\)の範囲がそれぞれの\(k\)についてすべて出そろいました。
最後に、\(k\)はもともと\(x\)なので、\(k→x\)に戻して領域を図示します。
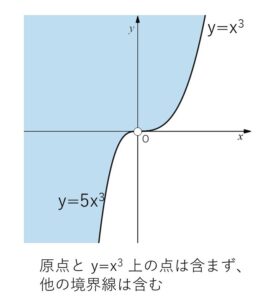
\(k\)を\(x\)に戻してまとめて図示すると次の通り。
\(x<0\) のとき \(y≧5x^3\)
\(x=0\) のとき \(y>0\)
\(x>0\) のとき \(y>x^3\)
(解法 ii) 逆像法
これに対して、\(x,y\)に対応する\(t\)が存在するかどうかに着目するのが逆像法です。
例えば、\((x,y)=(1,5)\)を
\(y=t^3+3xt^2+x^3\)・・・①
に代入すると、\(5=t^3+3t^2+1\) よりこの\(t\)の方程式を解くと、
\((t-1)(t+2)^2=0\) より、\(t=1,-2\) となるので、\(t=1\)が正の数としてとれます。よって\(t=1\)とすれば\((x,y)=(1,5)\)が①を満たすことになるので、点\((1,5)\)が①を通ることになります。
次に、\((x,y)=(1,1)\)を①に代入すると、
\(1=t^3+3t^2+1\) よりこの\(t\)の方程式を解くと、
\(t^2(t+3)=0\) より、\(t=-3,0\) となるので、正の数\(t\)がとれません。\((1,1)\)を通るようにするには\(t=-3,0\)とするしかないので(もし他の\(t\)があるなら方程式の解としてでてくるはずだから)、どのように\(t\)を正の範囲で動かしても\((1,1)\)を通ることはないことになります。
このように他の\((x,y)\)についても対応する正の数\(t\)があるかどうか同様に調べていくのですが、これも具体的に挙げていくとキリがないので、\(x,y\)を文字のままおいて(文字定数として扱う)、\(t\)の3次方程式①が正の範囲で実数解をもつような\(x,y\)を考えていくことになります。
①を\(t\)の3次方程式とみる
\(t^3+3xt^2+x^3-y=0\)・・・①
この\(t\)の方程式が少なくとも1つの正の実数解をもつ\(x,y\)の条件を考えればよい。
\(g(t)=t^3+3xt^2+x^3-y\) とおくと、グラフが \(t>0\) の範囲で\(t\)軸と共有点を少なくとも1つもつときを考えればよい。
\(g'(t)=3t(t+2x)\)
\(g'(t)=0\) となるのは、\(t=0,-2x\)
(ア)\(x=0\) のとき
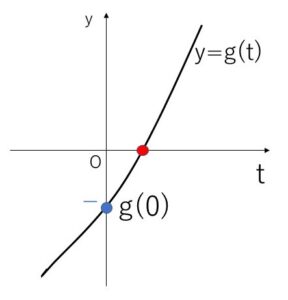
\(g'(t)=3t^2≧0\) より単調増加になるから、正の部分で共有点をもつには
\(g(0)<0\)
よって
\(x^3-y<0\)
\(x=0\)だから、つまり
\(y>0\)
(イ)\(x≠0\) のとき
\(x<0\), \(x>0\) の増減表は次の通り。
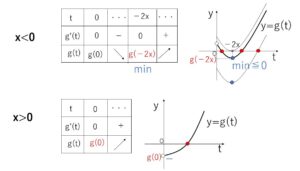
したがって、\(y=g(t)\)が\(t\)軸の正の部分で共有点を持つ場合は
\(x<0\) のとき \(g(-2x)=5x^3-y≦0\)
\(x>0\) のとき \(g(0)=x^3-y<0\)
以上をまとめると
\(x<0\) のとき \(y≧5x^3\)
\(x=0\) のとき \(y>0\)
\(x>0\) のとき \(y>x^3\)
図は(解法i)と同様になる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→微分法と軌跡・領域② back→高次方程式の実数解のとりうる範囲