引き続き微分を利用する軌跡・領域問題について見ていきます。
解法の考え方の詳細は
前回 →(5-8)微分法と軌跡・領域①
図形と方程式 →(5-11)通過領域①
を参照してください
(例題1)
実数\(t\)が \(t≧0\) を動くとき、直線 \(y=3t^2x-2t^3\) が通る平面上の点の集合を\(A\)とする。このとき、点\(P(a,b)\) に対して \(P \in A\) となるための必要十分条件を求めよ。ただし、\(a>0\) とする。
\(A\)は直線が通る領域で、\(P(a,b)\)は\(xy\)平面上の点です。必要十分条件を求めよと言っているので
①「条件\(s\):(\(a,b\)の条件)」 → 「 \(P(a,b) \in A\)」 が成り立ち (条件\(s\)は十分条件)
②「\(P(a,b) \in A\)」 → 「条件\(s\):(\(a,b\)の条件)」も成り立つ (条件\(s\)は必要条件)
ということですが、\(a,b\)の条件が表す領域が \(A\)の一部分だと①が成り立ちますが②が成り立たず、\(a,b\)の条件が表す領域が \(A\)を含み\(A\)より広い領域だと②が成り立ちますが①が成り立たちません。つまり①②両方が成り立つためには\(a,b\)の条件が表す領域がピッタリ\(A\)に一致しなければならないということで、その条件が求める答えです。
問題文の言い回しが難しいですが、要するに「直線 \(y=3t^2x-2t^3\) が動く領域を式で表せ」と言っているだけの問題です。今回も順像法と逆像法の2パターンで解いてみたいと思います。
(解法1)順像法
直線上の点を\((a,b)\)として
直線 \(b=3t^2a-2t^3\) (\(t≧0\)) が通る領域を表す\(a,b\)の条件を求めればよい。
\(f(t)=-2t^3+3at^2\) とおいて、\(a=k\)で固定すると
\(f(t)=-2t^3+3kt^2\)
\(f'(t)=-6t(t-k)\)
\(f'(t)=0\) となるのは \(t=0,k\)
\(a>0\) より \(k>0\) だから、\(b=f(t)\) の増減表は次の通り。
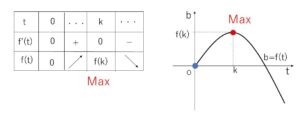
したがって\(b=f(t)\)のとりうる範囲は
\(b≦f(k)=k^3\)
\(k\)を\(a\)に戻すと
\(b≦a^3\)
(解法2)逆像法
直線上の点を\((a,b)\)として
直線 \(b=3t^2a-2t^3\) (\(t≧0\)) が通る領域を表す\(a,b\)の条件を求めればよい。
よって\(t\)についての3次方程式
\(2t^3-3at^2+b=0\)
が \(t≧0\) の範囲に少なくとも1つの実数解をもつ条件
つまり、\(g(t)=2t^3-3at^2+b\) が \(t\)軸と\(0\)以上の部分で共有点を少なくとも1つもつ条件を考えればよい。
\(g'(t)=6t(t-a)\) より
\(g'(t)=0\) となるのは、\(t=0,a\)
問題文の条件 \(a>0\) より増減表は次の通り。
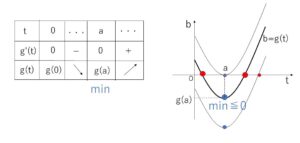
したがって求める\(a,b\)の条件は
\(g(a)≦0\)
\(-a^3+b≦0\)
\(b≦a^3\)
(例題2)
実数\(a\)が \(0<a<1\) の範囲を動くとき、曲線 \(y=x^3-3a^2x+a^2\) の極大点と極小点の間にある部分(ただし、極大点,極小点は含まない) が通る範囲を図示せよ。
まずは極値をとる\(x\)座標を求めるために\(x\)で微分します。
(解法1)順像法
\(y’=3(x+a)(x-a)\) より
\(y’=0\)となるのは \(x=±a\)
\(0<a<1\) だから、\(x=±a\) で極値をとる。
よって、\(0<a<1\) の範囲で\(a\)を動かしたときに
曲線 \(y=x^3-3a^2x+a^2\) の \(-a<x<a\) の部分 が通過する範囲を求めればよい。
順像法による解法では\(x=k\) で固定しますが、その\(k\)は \(-a<k<a\) の範囲ないといけません。そして一応断っておくとこの範囲が\(a\)によって表されているので\(a\)が動くと範囲も動きます。この\(k\)の範囲は、\(-1<x<1\) の内部にある原点対称の領域なのでイメージはしやすいと思います。(これらのことはあとで\(a\)について整理するのでそこまで意識する必要はありませんが)
それと、\(x=k\)(定数)と固定して\(a\)を動かすので、これから考えるのは\(a\)を変数とする関数です(\(a\)の2次関数になります)。したがって\(a\)が主役となることを意識しつつ、出てくる式をすべて\(a\)について整理していきます。
\(x=k\) と固定すると
曲線は \(y=k^3-3a^2k+a^2\)・・・①
また、\(-a<k<a\)・・・②
①②を\(a\)について整理して、②については\(0<a<1\)と合わせると
\(y=(1-3k)a^2+k^3\)・・・③
\(0<a<1\) かつ \(a>-k\) かつ \(a>k\) ・・・④
そして、\(0<a<1\) より \(k\)のとりうる範囲は②より
\(-1<k<1\)・・・⑤ となるのでこの範囲で固定していく。
また ④の \(a>-k\) かつ \(a>k\) は\(k\)の正負で変化するので、これも考慮していきます。
(ア)\(1-3k>0\) つまり \(k<\displaystyle\frac{1}{3}\) のとき
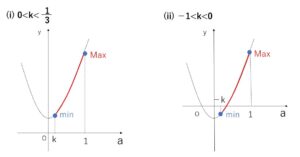
(i)\(0<k<\displaystyle\frac{1}{3}\) のとき
\(a\)の範囲④の共通部分は
\(k<a<1\)
\(y=(1-3k)a^2+k^3\)・・・③ が下に凸の関数で、軸は\(a=0\) だから\(y\)のとりうる範囲は
\((1-3k)k^2+k^3<y<(1-3k)1^2+k^3\)
整理して
\(-2k^3+k^2<y<k^3-3k+1\)
(ii)\(-1<k<0\) のとき
\(a\)の範囲④の共通部分は
\(-k<a<1\)
(i)とグラフの形状は同様だから
\((1-3k)(-k)^2+k^3<y<(1-3k)1^2+k^3\)
整理して
\(-2k^3+k^2<y<k^3-3k+1\)
(イ)\(1-3k=0\) つまり \(k=\displaystyle\frac{1}{3}\) のとき
\(a\)の範囲④の共通部分は
\(\displaystyle\frac{1}{3}<a<1\)
\(a\)の関数③は
\(y=k^3\)
定数関数だから\(y\)のとりうる範囲は
\(y\)\(=k^3=(\displaystyle\frac{1}{3})^3\)\(=\displaystyle\frac{1}{27}\)
(ウ)\(1-3k<0\) つまり \(k>\displaystyle\frac{1}{3}\) のとき
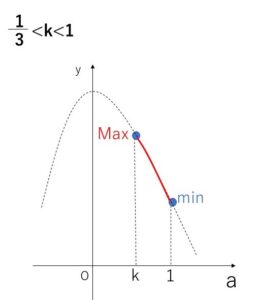
\(k<1\)とあわせると、\(\displaystyle\frac{1}{3}<k<1\) で
\(a\)の範囲④の共通部分は
\(k<a<1\)
\(y=(1-3k)a^2+k^3\)・・・③ が上に凸の関数で、軸は\(a=0\) だから\(y\)のとりうる範囲は
\((1-3k)1^2+k^3<y<(1-3k)k^2+k^3\)
整理して
\(k^3-3k+1<y<-2k^3+k^2\)
(ア)~(ウ)より \(k\)を\(x\)に戻してまとめると
\(-1<x<\displaystyle\frac{1}{3}\) のとき \(-2x^3+x^2<y<x^3-3x+1\)
\(x=\displaystyle\frac{1}{3}\) のとき \(y=\displaystyle\frac{1}{27}\)
\(\displaystyle\frac{1}{3}<x<1\) のとき \(x^3-3x+1<y<-2x^3+x^2\)
上記領域を図示すると次の通り。
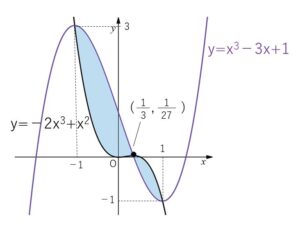
境界線上の点は \((\displaystyle\frac{1}{3},\displaystyle\frac{1}{27})\) のみ含む
\(0<a<1\) かつ \(|k|<a\)となり、 さらに ⑤より\((0<)|k|<1\) となるので、この2つの共通範囲を求めると、結局④は \(|k|<a<1\) とキレイにまとめることができます。こうすると場合分けなどが少し楽になります。
続いて逆像法の解法です。
(解法2)逆像法
極値をとる\(x\)の値は、(解法1)と同様に微分すると
\(x=±a\) と得られる。
曲線の方程式を\(a\)の方程式とみて
\((1-3x)a^2+x^3-y=0\)・・・(1) とすると
方程式(1)が 「\(0<a<1\) かつ \(|x|<a\)」・・・(2)
の範囲に実数解をもつような\(x,y\)の条件を求めれば、この\(x,y\)の条件が表す領域が、曲線の通過領域となる。
\(x\)のとりうる範囲は極値間の範囲を考えると、
\(-1<x<1\) ・・・(3)となるので、(2)は
「\(|x|<a<1\)」・・・(4) とまとめることができる。
ここで、\(a^2=t\) とすると、(1)(4)は次のように置き換わる。
((4)は辺々2乗する)
\((1-3x)t+x^3-y=0\)・・・(5)
\(x^2<t<1\)・・・(6)
よって\(t\)の1次方程式が(5)が、(6)の範囲で実数解をもつような\(x,y\)の条件を考えればよい。
\(f(t)=(1-3x)t+x^3-y\) とおいて、このグラフが(6)の範囲で\(t\)軸と共有点をもてばよく、
\(-1<x<1\) に注意すると
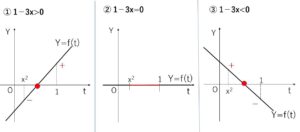
①\(1-3x>0\) つまり \(-1<x<\displaystyle\frac{1}{3}\) のとき
\(f(t)\)は右上がりのグラフとなるから
\(f(x^2)<0\) かつ \(f(1)>0\)
\((1-3x)x^2+x^3-y<0\) かつ \((1-3x)+x^3-y>0\) より
\(-2x^3+x^2<y<x^3-3x+1\)
②\(1-3x=0\) つまり \(x=\displaystyle\frac{1}{3}\) のとき
\(f(t)\)は定数関数となるから
\(f(t)=0\)
\(x^3-y=0\)
よって
\(y\)\(=(\displaystyle\frac{1}{3})^3\)\(=\displaystyle\frac{1}{27}\)
③\(1-3x<0\) つまり \(\displaystyle\frac{1}{3}<x<1\) のとき
\(f(t)\)は右下がりのグラフとなるので
\(f(x^2)>0\) かつ \(f(1)<0\)
\((1-3x)x^2+x^3-y>0\) かつ \((1-3x)+x^3-y<0\) より
\(x^3-3x+1<y<-2x^3+x^2\)
①~③をまとめると
\(-1<x<\displaystyle\frac{1}{3}\) のとき\(-2x^3+x^2<y<x^3-3x+1\)
\(x=\displaystyle\frac{1}{3}\) のとき \(y=\displaystyle\frac{1}{27}\)
\(\displaystyle\frac{1}{3}<x<1\) のとき \(x^3-3x+1<y<-2x^3+x^2\)
(領域図示は(解法1)と同様なので省略)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→曲線と円の共有点の個数 back→微分法と軌跡・領域①