曲線と円の共有点の個数に関する問題について見ていきます。
(例題)
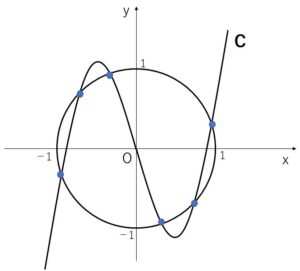
\(a\) を正の実数とする。座標平面上の曲線\(C\)を \(y=ax^3-2x\) で定める。原点を中心とする半径\(1\)の円と\(C\)の共有点の個数が\(6\)個であるような\(a\)の範囲を求めよ。
(解答)
円: \(x^2+y^2=1\)・・・①
\(C\): \(y=ax^3-2x\)・・・②
②を①に代入して
\(x^2+(ax^3-2x)^2=1\)・・・③
\(x\)について整理すると
\(a^2x^6-4ax^4+5x^2-1=0\)・・・④
\(t=x^2\) とおくと ④は
\(a^2t^3-4at^2+5t-1=0\)・・・⑤
(i)\(t<0\) のときは \(x\)は実数でない (\(x\)は0個)
(ii)\(t=0\) のときは \(x=0\) (\(x\)は1個)
(iii)\(t>0\) のときは \(x=±\sqrt{t}\) (\(x\)は2個)
(iv)\(t\)が虚数のときは \(x\)も虚数 (\(x\)は0個)
と対応していることと、⑤の方程式は最大でも解が3個しかとれないことから、\(x\)の方程式④が異なる6つの実数解をもつには、\(t\)の方程式⑤が異なる3つの正の実数解をもてばよいことになります。
円と曲線\(C\)が6つの共有点をもつには、\(x\)の方程式④が6つの異なる実数解をもてばよい。
そして、\(t=x^2\) より、\(t\)の方程式⑤が異なる3つの正の実数解をもてばよいことになる。
\(f(t)=a^2t^3-4at^2+5t-1\) とおいて、
\(t>0\)の範囲で\(t\)軸と3つの共有点をもつ条件を考えると
\(f'(t)=3a^2t^2-8at+5\)\(=(at-1)(3at-5)\) より
\(f'(t)=0\) となるのは、\(\displaystyle\frac{1}{a},\displaystyle\frac{5}{3a}\)
\(a>0\) より \(\displaystyle\frac{1}{a}<\displaystyle\frac{5}{3a}\) だから増減表は次の通り。
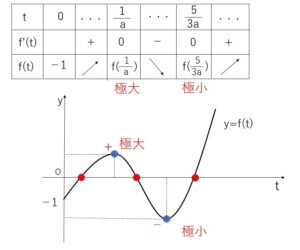
よって、3つの共有点をもつ条件は
\(f(\displaystyle\frac{1}{a})>0\) かつ \(f(\displaystyle\frac{5}{3a})<0\) となるから
\(\displaystyle\frac{1}{a}-\displaystyle\frac{4}{a}+\displaystyle\frac{5}{a}-1>0\) かつ \(\displaystyle\frac{125}{27a}-\displaystyle\frac{100}{9a}+\displaystyle\frac{25}{3a}-1<0\)
\(\displaystyle\frac{2}{a}>1\) かつ \(\displaystyle\frac{50}{27a}<1\)
したがって
\(\displaystyle\frac{50}{27}<a<2\)
※\(t≦1\) という制限 の有無について
\(t\)が正の実数ならば、\(x^2=t\) より \(x\)も実数となり、もともとの\(x\)の方程式
\(x^2+(ax^3-2x)^2=1\)・・・③
の \(x\) と \(ax^3-2x\) のどちらも実数になるので、③が成り立つとき
\(-1≦x≦1\), \(-1≦ax^3-2x≦1\)
が保証されるので(もしこの範囲にないと左辺が\(1\)を超えてしまう)、\(-1≦x≦1\) つまり \(t≦1\)という制限が必要ないことになります。
ちなみに \(t≦1\) を追加すると、
極値をとる\(x\)のうち大きい方の \(x=\displaystyle\frac{5}{3a}\) について \(\displaystyle\frac{5}{3a}<1\) つまり \(a>\displaystyle\frac{5}{3}\)
\(f(1)≧0\) つまり \(a^2-4a+4≧0\) \(⇔\) \((a-2)^2≧0\) (常に成り立つ)
の2つの条件が加わりますが、答えに影響はないです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→微分法と軌跡・領域②