面積の計算①(基礎)

積分を利用した具体的な面積計算の演習です。

(例題1)
(1)放物線 \(y=6x^2-9x-6\) と\(x\)軸 および 直線 \(x=-2\) で囲まれた2つの部分の面積の和を求めよ。
(2)曲線 \(y=x^3-3x^2+2x\) と \(x\)軸とで囲まれた部分の面積を求めよ。
(3)2つの3次関数 \(y=x^3-2x\), \(y=2x^3-3x^2\) のグラフで囲まれた図形の面積を求めよ。

(解答)
(1)

\(6x^2-9x-6=0\) を解くと
\(3(2x+1)(x-2)=0\)
\(x=-\displaystyle\frac{1}{2},2\)

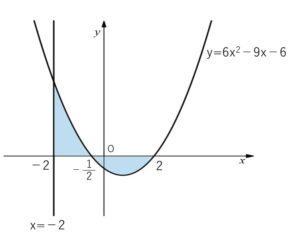
図より面積\(S\)は
\(S=\displaystyle\int_{-2}^{-\frac{1}{2}}(6x^2-9x-6)dx+\displaystyle\int_{-\frac{1}{2}}^{2}-(6x^2-9x-6)dx\)
\(=\left[2x^3-\displaystyle\frac{9}{2}x^2-6x\right]_{-2}^{-\frac{1}{2}}+\displaystyle\int_{-\frac{1}{2}}^{2}-6(x+\displaystyle\frac{1}{2})(x-2)dx\)
\(=(-\displaystyle\frac{1}{4}-\displaystyle\frac{9}{8}+3)-(-16-18+12)+(-6)\cdot(\displaystyle\frac{-1}{6})(2+\displaystyle\frac{1}{2})^3\)
\(=-\displaystyle\frac{11}{8}+3+22+\displaystyle\frac{125}{8}\)
\(=\displaystyle\frac{157}{4}\)

(2)

\(y=x^3-3x^2+2x=x(x-1)(x-2)\) より
グラフと\(x\)軸の交点の\(x\)座標は、\(x=0,1,2\)

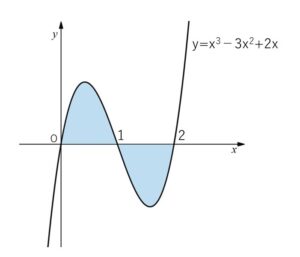
図より面積\(S\)は
\(S=\displaystyle\int_0^1(x^3-3x^2+2x)dx+\displaystyle\int_1^2-(x^3-3x^2+2x)dx\)
\(=\left[\displaystyle\frac{1}{4}x^4-x^3+x^2\right]_0^1+\left[\displaystyle\frac{1}{4}x^4-x^3+x^2\right]_2^1\)　(2つめの積分区間を入れ替えた)
\(=\displaystyle\frac{1}{4}×2-(4-8+4)\)
\(=\displaystyle\frac{1}{2}\)

(3)

\(y=(2x^3-3x^2)-(x^3-2x)\)
\(=x^3-3x^2+2x\)
\(=x(x-1)(x-2)\)

(2)と同じで面積は \(\displaystyle\frac{1}{2}\)

ちなみにもとの2つグラフを図示すると次の通りです。

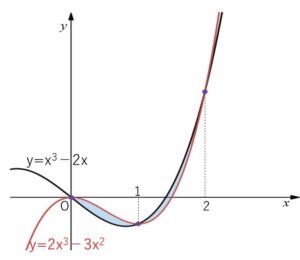
(例題2)
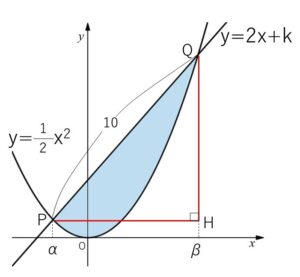
放物線 \(y=\displaystyle\frac{1}{2}x^2\) と 直線 \(y=2x+k\) は2点\(P,Q\)で交わり、線分\(PQ\)の長さは\(10\)であるという。
(1)\(k\)の値を求めよ。
(2)この放物線と直線とで囲まれる部分の面積を求めよ。

(解答)
(1)

2つの方程式から\(y\)を消去して
\(\displaystyle\frac{1}{2}x^2=2x+k\)
\(\displaystyle\frac{1}{2}x^2-2x-k=0\)・・・①

方程式①の2解を\(α,β\) (\(α<β\)) とすると、これらは交点の\(x\)座標になる。

2つの交点をもつことから、①が異なる2つの実数解をもつので
\(D=4+2k>0\)
\(k>-2\)・・・②

また解と係数の関係から
\(α+β=4\), \(αβ=-2k\)

図の
\(PH=β-α\)
\(QH=(2β+k)-(2α+k)=2(β-α)\)
より
\(PQ^2=(β-α)^2+\{2(β-α)\}^2=5(β-α)^2\)

ここで
\((β-α)^2=α^2+β^2-2αβ\)
\(=(α+β)^2-4αβ\)
\(=16+8k\) より

\(10^2=5(16+8k)\)
したがって
\(k=\displaystyle\frac{1}{2}\)　(②\(k>-2\)を満たす)

(2)

面積\(S\)は
\(S=\displaystyle\int_α^β(2x+\displaystyle\frac{1}{2}-\displaystyle\frac{1}{2}x^2)dx\)
\(=\displaystyle\int_α^β-\displaystyle\frac{1}{2}(x-α)(x-β)dx\)
\(=(-\displaystyle\frac{1}{2})(-\displaystyle\frac{1}{6})(β-α)^3\)
\(=\displaystyle\frac{1}{12}(β-α)^3\)

(1)より
\((β-α)^2=16+8k=20\)
\(β>α\) より
\(β-α=2\sqrt{5}\)

したがって
\(S=\displaystyle\frac{1}{12}(2\sqrt{5})^3\)
\(=\displaystyle\frac{10\sqrt{5}}{3}\)

(例題3)
次の連立不等式の表す領域の面積を求めよ。
\(y≧2x^2\)
\(2x+2≦y≦2x+4\)

(解答)
\(y=2x^2\) と \(y=2x+4\) より\(y\)を消去して
\(2x^2=2x+4\)
\((x-2)(x+1)=0\)
\(x=2,-1\)

\(y=2x^2\) と \(y-2x+2\) より \(y\)を消去して
\(2x^2=2x+2\)
\(x^2-x-1=0\)
\(x=\displaystyle\frac{1±\sqrt{5}}{2}\)
(これを\(α,β\) (\(α<β\)) とおくと)
\(β-α=\sqrt{5}\)

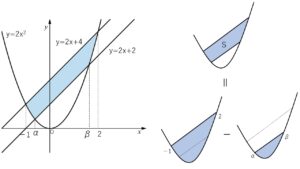
求める面積\(S\)は、\(y=2x^2\) と \(y=2x+4\) の囲む図形の面積」から、
「\(y=2x^2\) と \(y=2x+2\) の囲む図形の面積」を除いたものになるので

\(S=\displaystyle\int_{-1}^{2}(2x+4-2x^2)dx-\displaystyle\int_{α}^{β}(2x+4-2x^2)dx\)
\(=\displaystyle\int_{-1}^{2}-2(x+1)(x-2)dx+\displaystyle\int_{α}^{β}2(x-α)(x-β)dx\)
\(=\displaystyle\frac{2}{6}(2+1)^3-\displaystyle\frac{2}{6}(β-α)^3\)
\(=9-\displaystyle\frac{5\sqrt{5}}{3}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→面積の計算②　back→定積分と面積の関係