奇関数・偶関数の定積分について見ていきます。
・奇関数・偶関数の定積分
上端と下端の絶対値が等しく、符号が反対の積分について次の等式が成り立ちます。
\(n\)を自然数として
\(\displaystyle\int_{-a}^ax^{2n-1}dx=0\) (奇関数)
\(\displaystyle\int_{-a}^ax^{2n}dx=2\displaystyle\int_{0}^ax^{2n}dx\) (偶関数)
\(y=x^{2n-1}\), \(y=x^{2n}\) のグラフを書いて面積を考えれば明らかです。
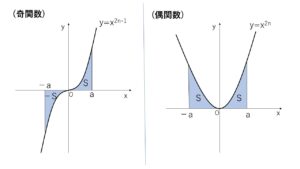
数式による証明は以下の通りです。
(証明)
(奇関数)
\(\displaystyle\int_{-a}^ax^{2n-1}dx\)
\(=\left[\displaystyle\frac{1}{2n}x^{2n}\right]_{-a}^a\)
\(=\displaystyle\frac{1}{2n}a^{2n}-\displaystyle\frac{1}{2n}(-a)^{2n}\)
\(=\displaystyle\frac{1}{2n}a^{2n}-\displaystyle\frac{1}{2n}a^{2n}\)
\(=0\)
(偶関数)
(左辺)
\(=\displaystyle\int_{-a}^ax^{2n}dx\)
\(=\left[\displaystyle\frac{1}{2n+1}x^{2n+1}\right]_{-a}^a\)
\(=\displaystyle\frac{1}{2n+1}a^{2n+1}-\displaystyle\frac{1}{2n+1}(-a)^{2n+1}\)
\(=\displaystyle\frac{1}{2n+1}a^{2n+1}+\displaystyle\frac{1}{2n+1}a^{2n+1}\)
\(=\displaystyle\frac{2}{2n+1}a^{2n+1}\)
(右辺)
\(=2\displaystyle\int_{0}^ax^{2n}dx\)
\(=2\left[\displaystyle\frac{1}{2n+1}x^{2n+1}\right]_{0}^a\)
\(=\displaystyle\frac{2}{2n+1}a^{2n+1}\)
よって
(左辺)=(右辺) が成り立つ。
(例題1)
次の定積分を求めよ。
\(\displaystyle\int_{-2}^{2}(x^4-2x^3+3x^2-3x+5)dx\)
\(x^{奇数}\) の部分は全部\(0\)になるので無視できます。
(解答)
\(\displaystyle\int_{-2}^{2}(x^4-2x^3+3x^2-3x+5)dx\)
\(=2\displaystyle\int_{0}^{2}(x^4+3x^2+5)dx\)
\(=2\left[\displaystyle\frac{1}{5}x^5+x^3+5x\right]_0^2\)
\(=2(\displaystyle\frac{32}{5}+8+10)\)
\(=\displaystyle\frac{244}{5}\)
(例題2)
整式 \(g_1(x)=x-k\), \(g_2(x)=x+1\), \(g_3(x)=x^2+lx+m\) (\(k,l,m\) は定数) が、
\(\displaystyle\int_{-1}^1g_1(x)g_2(x)dx=\displaystyle\int_{-1}^1g_2(x)g_3(x)dx=\displaystyle\int_{-1}^1g_3(x)g_1(x)dx=0\)
を満たすという。\(k,l,m\)の値を求めよ。
(解答)
\(\displaystyle\int_{-1}^1g_1(x)g_2(x)dx\)
\(=\displaystyle\int_{-1}^1(x-k)(x+1)dx\)
\(=2\displaystyle\int_{0}^1(x^2-k)dx\)
\(=2\left[\displaystyle\frac{1}{3}x^3-kx\right]_{0}^1\)
\(=2(\displaystyle\frac{1}{3}-k)\)
よって
\(\displaystyle\frac{1}{3}-k=0\)・・・①
\(\displaystyle\int_{-1}^1g_2(x)g_3(x)dx\)
\(=\displaystyle\int_{-1}^1(x+1)(x^2+lx+m)dx\)
\(=2\displaystyle\int_{0}^1\{(l+1)x^2+m\}dx\)
\(=2\left[\displaystyle\frac{l+1}{3}x^3+mx\right]_{0}^1\)
\(=2(\displaystyle\frac{l+1}{3}+m)\)
よって
\(\displaystyle\frac{l+1}{3}+m=0\)・・・②
\(\displaystyle\int_{-1}^1g_3(x)g_1(x)dx\)
\(=\displaystyle\int_{-1}^1(x^2+lx+m)(x-k)dx\)
\(=2\displaystyle\int_{0}^1\{(l-k)x^2-km\}dx\)
\(=2\left[\displaystyle\frac{l-k}{3}x^3-kmx\right]_{0}^1\)
\(=2(\displaystyle\frac{l-k}{3}-km)\)
よって
\(\displaystyle\frac{l-k}{3}-km=0\)・・・③
①②③より
\(k=\displaystyle\frac{1}{3}\), \(l=0\), \(m=-\displaystyle\frac{1}{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→面積比・面積の等分 back→面積の計算②