面積比(面積の等分)に関する問題について見ていきます。
(例題1)
曲線 \(y=-x(x-4)\) と 直線 \(y=ax\), \(y=bx\) (\(0<a<b<4\)) がある。
この2直線により、曲線と\(x\)軸とで囲まれた部分は3つの部分に分類される。この3つの部分の面積が等しいとき、\((4-b)^3\), \((4-a)^3\) の値を求めよ。
直線と曲線の交点を求めて図示していきます。
(解答)
\(-x(x-4)=ax\) を解くと
\(x(x+a-4)=0\) より
\(x=0,4-a\)
\(-x(x-4)=bx\) を解くと
\(x(x+b-4)=0\)
\(x=0,4-b\)
\(0<4-b<4-a<4\) より曲線と2直線を図示すると次の通り。
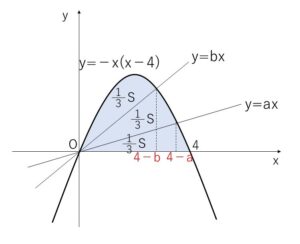
\((4-b)^3\)という値は、曲線と\(y=bx\)の囲む面積を1/6公式を使って求めると出てきて、この図形の面積は図より\(\displaystyle\frac{1}{3}S\)です。
\((4-a)^3\)も同様で、こちらは図より \(\displaystyle\frac{2}{3}S\) です。
\(y=-x(x-4)\) と \(x\)軸で囲まれた面積を\(S\)とすると
\(S=\displaystyle\int_0^4-x(x-4)dx\)
\(=\displaystyle\frac{1}{6}(4-0)^3\)
\(=\displaystyle\frac{32}{3}\)
\(y=-x(x-4)\) と \(y=bx\)で囲まれた面積は図より\(\displaystyle\frac{1}{3}S\)だから
\(\displaystyle\frac{1}{3}S\)\(=\displaystyle\int_0^{4-b}\{-x(x-4)-bx\}dx\)
\(=\displaystyle\int_0^{4-b}-\{x(x+b-4)\}dx\)
\(=\displaystyle\frac{1}{6}(4-b)^3\)
よって
\(\displaystyle\frac{1}{6}(4-b)^3=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{32}{3}\)
\((4-b)^3=\displaystyle\frac{64}{3}\)
また、\(y=-x(x-4)\) と \(y=ax\)で囲まれた面積は図より\(\displaystyle\frac{2}{3}S\)だから
\(\displaystyle\frac{2}{3}S\)\(=\displaystyle\int_0^{4-a}\{-x(x-4)-ax\}dx\)
\(=\displaystyle\int_0^{4-a}-\{x(x+a-4)\}dx\)
\(=\displaystyle\frac{1}{6}(4-a)^3\)
よって
\(\displaystyle\frac{1}{6}(4-a)^3=\displaystyle\frac{2}{3}\cdot\displaystyle\frac{32}{3}\)
\((4-a)^3=\displaystyle\frac{128}{3}\)
(例題2)
2つの関数
\(f(x)=x^3-(2a+1)x^2+a(a+1)x\)
\(g(x)=x^2-ax\)
(ただし、 \(a>0\)) について、次の問いに答えよ。
(1)2つの曲線 \(y=f(x)\), \(y=g(x)\) の交点の座標をすべて求めよ。
(2)2つの曲線が囲む2つの部分の面積が等しいときの\(a\)の値を求めよ。
(解答)
(1)
\(f(x)=g(x)\)
つまり
\(f(x)-g(x)=0\) を解くと
\(x^3-(2a+1)x^2+a(a+1)x-(x^2-ax)=0\)
\(x\{x^2-(2a+2)x+a(a+2)\}=0\)
\(x(x-a)\{x-(a+2)\}=0\)
\(x=0,a,a+2\)
それぞれ \(y=g(x)\) に代入して
\(g(0)=0\)
\(g(a)=0\)
\(g(a+2)=2(a+2)\)
したがって交点の座標は
\((0,0)\), \((a,0)\) \((a+2,2(a+2))\)
(2)
また3交点の\(x\)座標は、\(a>0\) より \(0<a<a+2\) の順番で並びます。
2つの曲線の囲む面積は、
\(y=f(x)-g(x)=x(x-a)\{x-(a+2)\}\)
と\(x\)軸の囲む面積と同じである。
\(0<a<a+2\) より、\(y=f(x)-g(x)\)のグラフは次の通り。
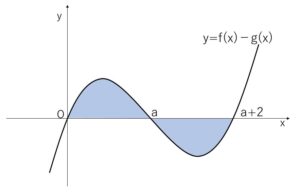
2つの部分の面積が等しいので、
\(\displaystyle\int_{0}^{a}\{f(x)-g(x)\}dx=\displaystyle\int_{a}^{a+2}-\{f(x)-g(x)\}dx\)
左辺によせて2つの積分を合わせると
\(\displaystyle\int_{0}^{a+2}\{f(x)-g(x)\}dx=0\)・・・①
よって
\(\displaystyle\int_0^{a+2}\{x^3-(2a+2)x^2+a(a+2)x\}dx=0\)
\(\left[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{2a+2}{3}x^3+\displaystyle\frac{a(a+2)}{2}x^2\right]_0^{a+2}=0\)
\(\displaystyle\frac{1}{4}(a+2)^4-\displaystyle\frac{2a+2}{3}(a+2)^3+\displaystyle\frac{a(a+2)}{2}(a+2)^2=0\)
(12倍して)
\((a+2)^3\{3(a+2)-4(2a+2)+6a\}=0\)
\((a+2)^3(a-2)=0\)
\(a>0\) より
\(a=2\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→接線と面積① back→奇関数・偶関数の定積分