定積分と体積の関係

体積と定積分の関係について見ていきます。

・定積分と体積の関係
ある立体の平行な2つの平面に挟まれた部分の体積の体積は、定積分により求めることができます。

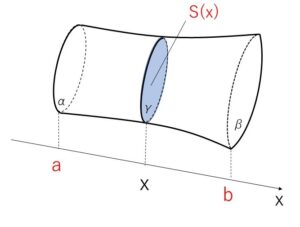
2つの平面\(α,β\)に垂直な直線を\(x\)軸にとって、\(x\)軸と平面\(α,β\) との交点の座標を、それぞれ\(a,b\) (\(a<b\)) とします。\(a≦x≦b\) としたときの、\(x\)軸に垂直で\(x\)軸との交点の座標が\(x\)である平面\(γ\)で立体を切断したときの断面積を\(S(x)\)とすると、立体の体積\(V\)は次のように表されます。

\(V=\displaystyle\int_{a}^{b}S(x)dx\)

(解説)

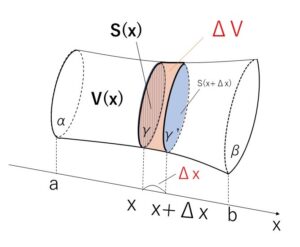
断面積は、\(x\)を1つ決めるとただ1つ決まるので\(x\)の関数で表され、\(S(x)\)とおける。
平面\(α,γ\)で挟まれる部分の立体の体積も同様に、\(V(x)\)とおける。

\(x\)の増分を\(Δx\) (\(Δx>0\))として、これに対する\(V(x)\)の増分を\(ΔV\)とすると、\(ΔV\)は \(x,x+Δx\) を通る2つの平面\(γ,γ’\) の間にある部分の体積となる。

\(Δx\)が十分小さいとき、\(ΔV\)は、「底面積\(S(x)\)、高さ\(Δx\)の柱状の立体の体積」に近似できるので

\(ΔV≒S(x)Δx\)・・・①

よって
\(\displaystyle\frac{ΔV}{Δx}≒S(x)\)・・・②

\(Δx\)を限りなく\(0\)に近づけると、①の両辺は限りなく近づくので、②の両辺も限りなく近づく。したがって

\(V'(x)=\displaystyle\lim_{Δx \to 0}\displaystyle\frac{ΔV}{Δx}=S(x)\)・・・③

(\(Δx<0\)のときも同様に③が成り立つ。このときは\(Δx\),\(ΔV\)ともに負の値になる)

ゆえに\(V(x)\)は\(S(x)\)の不定積分の1つになり、

\(V(b)-V(a)=\displaystyle\int_a^bS(x)dx\)

\(V(x)\)の定義から \(V(a)=0\), \(V(b)=V\) となるから

\(V=\displaystyle\int_a^bS(x)dx\)

※面積の導出のときと同じように、\(ΔV\)を「底面積\(S(t)\)、高さ\(Δx\)の柱状の立体の体積」に完全に置き換えてもよいです。

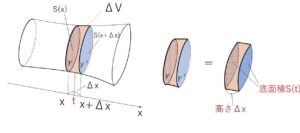
すなわち、\(x\)と\(x+Δx\) の間に適当な\(t\)をとり、

\(ΔV=S(t)Δx\)

とすれば

\(\displaystyle\frac{ΔV}{Δx}=S(t)\)

ここで、\(Δx→0\) とすると \(t→x\) つまり \(S(t)→S(x)\) なので

\(V'(x)=\displaystyle\lim_{Δx→0}\displaystyle\frac{ΔV}{Δx}=S(x)\)

あとは先ほどと同じ流れになります。

(例題)
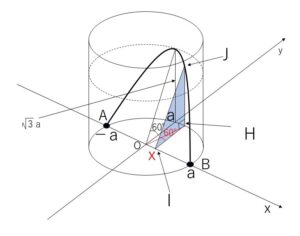
底面の半径が \(a\), 高さが \(2a\) の直円柱がある。この底面の直径\(AB\)を含み、底面と\(60°\)の傾きをなす平面で、直円柱を2つの部分に分ける。この2つの部分のうち、小さいほうの立体の体積を求めよ。

(解答)

\(-a≦x≦a\)　として

\(x\)軸との交点が\(x\)である、\(x\)軸に垂直な平面\(γ\)での断面を考える。

この平面\(γ\)で円柱を切断すると切り口は長方形になり、円柱を分ける平面が底面と\(60°\) の傾きをなしていることから、題意の小さいほうの立体を平面\(γ\)で切断したときの断面図は1つの角が\(60°\)の直角三角形\(IHJ\)になる。

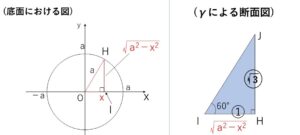
\(IH\)の長さは、斜辺\(a\)、底辺\(|x|\) の直角三角形\(OIH\) を考えると
\(IH=\sqrt{OH^2-OI^2}=\sqrt{a^2-x^2}\)

\(HJ\)の長さは、辺の比が \(1:\sqrt{3}\) であることから
\(HJ=\sqrt{3}IH=\sqrt{3}\cdot\sqrt{a^2-x^2}\)

したがって平面\(γ\)による小さいほうの立体の断面積\(S(x)\)は
\(S(x)=△IHJ\)
\(=\displaystyle\frac{1}{2}\cdot\sqrt{a^2-x^2}\cdot(\sqrt{3}\cdot\sqrt{a^2-x^2})\)
\(=\displaystyle\frac{\sqrt{3}}{2}(a^2-x^2)\)

ゆえに求める体積\(V\)は
\(V=\displaystyle\int_{-a}^{a}S(x)dx\)
\(=\displaystyle\frac{\sqrt{3}}{2}\displaystyle\int_{-a}^{a}(a^2-x^2)dx\)
\(=\sqrt{3}\displaystyle\int_{0}^{a}(a^2-x^2)dx\)
\(=\sqrt{3}\left[a^2x-\displaystyle\frac{1}{3}x^3\right]_{0}^{a}\)
\(=\displaystyle\frac{2\sqrt{3}}{3}a^3\)

(参考)
図では\(x\)軸に垂直な平面による切断面を考えるように誘導していますが、
\(y\)軸, \(z\)軸(\(xy\)平面に垂直な軸) に垂直な平面による切断面を考えても理屈上は体積が求まることになります。

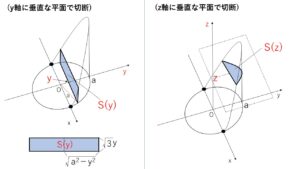
\(y\)軸に垂直な平面で切断した場合は、
\(S(y)=2\sqrt{3}y\sqrt{a^2-y^2}\) より
\(V=2\sqrt{3}\displaystyle\int_{0}^{a}y\sqrt{a^2-y^2}dy\)
となり、数Ⅲの積分が必要になります。

\(z\)軸に垂直な平面で切断した場合は、断面図は円の一部になりますが、これを\(z\)の関数で表すことは難しいです。(円の一部だから、さらに角の変数\(θ\)などを導入する必要がでてくる)

このように垂直な平面の選び方で計算の難度が変わってくるので、どの平面で切断するかの選択が重要になってきます。自由に選択できる場合には、図形が簡単なものになるようにするのが選択の目安です。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→回転体の体積①　back→円と曲線で囲まれた面積