ベクトルの垂直・平行と内積に関する演習です。
(例題1)
(1)\(\vec{a}=(4,2)\), \(\vec{b}=(3,-1)\), \(\vec{x}=(p,q)\) とする。\(\vec{x}\) と \(\vec{a}-\vec{b}\) は平行で、\(\vec{x}-\vec{b}\) と \(\vec{a}\) は垂直であるとき、\(p\)と\(q\)の値を求めよ。
(2)ベクトル \(\vec{a}=(3,-4)\) に垂直、平行である単位ベクトルをそれぞれ求めよ。
(解答)
(1)
平行: \(a_1b_2-a_2b_1=0\)
垂直: \(a_1b_1+a_2b_2=0\) (内積が\(0\))
です。ただし一方が \(\vec{0}\) でもこれらの等式が成り立つので、\(\vec{0}\)でないことの確認は必要です。
\(\vec{x}=(p,q)\), \(\vec{a}-\vec{b}=(1,3)\) と \(\vec{x}/\!/(\vec{a}-\vec{b})\) より
\(3p-q=0\)・・・①
また、\(\vec{x}-\vec{b}=(p-3,q+1)\), \(\vec{a}=(4,2)\) と \((\vec{x}-\vec{b})\perp\vec{a}\) より
\(4(p-3)+2(q+1)=0\)・・・②
①②より
\(p=1\), \(q=3\)
(このとき \(\vec{x}=(1,3)≠\vec{0}\), \(\vec{x}-\vec{b}=(-2,4)≠\vec{0}\) )
(2)
平行の場合も同じように解くこともできますが、ベクトルの実数倍は平行なベクトルであることを利用したほうが早いです。
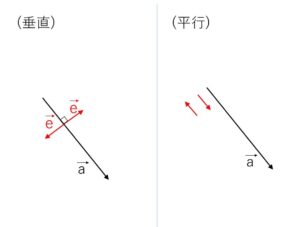
(垂直)
単位ベクトルを \(\vec{e}=(x,y)\) とおく。
大きさが\(1\)だから
\(\sqrt{x^2+y^2}=1\)
つまり
\(x^2+y^2=1\)・・・(i)
\(\vec{a}=(3,-4)\) に垂直だから
\(3x-4y=0\)・・・(ii)
(i)(ii) より
\(\vec{e}=(x,y)=(\displaystyle\frac{4}{5},\displaystyle\frac{3}{5}),(-\displaystyle\frac{4}{5},-\displaystyle\frac{3}{5})\)
(平行)
\(\vec{a}=(3,-4)\) の大きさは
\(|\vec{a}|=\sqrt{9+16}=5\)
よって
\(\vec{a}\)と同じ向きの単位ベクトルは、\(\displaystyle\frac{1}{5}(3,-4)\)
\(\vec{a}\)と反対向きの単位ベクトルは、\(-\displaystyle\frac{1}{5}(3,-4)\)
したがって求める単位ベクトルは
\((\displaystyle\frac{3}{5},-\displaystyle\frac{4}{5}),(-\displaystyle\frac{3}{5},\displaystyle\frac{4}{5})\)
(例題2)
\(|\vec{x}-\vec{y}|=1\), \(|2\vec{y}-\vec{x}|=2\), \((\vec{x}-\vec{y})\perp (2\vec{y}-\vec{x})\) のとき、\(\vec{x}\)と\(\vec{y}\)のなす角\(θ\) の余弦を求めよ。
(解答)
\(|\vec{x}-\vec{y}|^2=1^2\), \(|2\vec{y}-\vec{x}|^2=2^2\) より
\(|\vec{x}|^2-2\vec{x}\cdot\vec{y}+|\vec{y}|^2=1\)・・・①
\(|\vec{x}|^2-4\vec{x}\cdot\vec{y}+4|\vec{y}|^2=4\)・・・②
\((\vec{x}-\vec{y})\cdot(2\vec{y}-\vec{x})=0\) より
\(-|\vec{x}|^2+3\vec{x}\cdot\vec{y}-2|\vec{y}|^2=0\)・・・③
①+③, ②+③ より
\(\vec{x}\cdot\vec{y}-|\vec{y}|^2=1\)・・・④
\(-\vec{x}\cdot\vec{y}+2|\vec{y}|^2=4\)・・・⑤
④⑤より
\(|\vec{y}|^2=5\), \(\vec{x}\cdot\vec{y}=6\)
①より
\(|\vec{x}|^2=8\)
したがって
\(\cosθ=\displaystyle\frac{\vec{x}\cdot\vec{y}}{|\vec{x}||\vec{y}|}=\displaystyle\frac{6}{\sqrt{5}\cdot2\sqrt{2}}\)\(=\displaystyle\frac{3\sqrt{10}}{10}\)
(例題3)
2つのベクトル \(\vec{a}=(t+2,t^2-k)\), \(\vec{b}=(t^2,-t-1)\) が、どのような\(t\)の実数値に対しても垂直にならない実数\(k\)の値の範囲を求めよ。
ただし一方のベクトルが\(\vec{0}\)のときも 内積=0 となるので注意です(このとき垂直でない)。
(解答)
\(\vec{a}\cdot\vec{b}=0\) について
\((t+2)\cdot t^2+(t^2-k)\cdot(-t-1)=0\)
整理すると
\(t^2+kt+k=0\)・・・①
①を満たす実数\(t\)が存在しなければよいので
\(D<0\)
\(k^2-4k<0\)
\(k(k-4)<0\)
\(0<k<4\)
また、\(\vec{b}=(t^2,-t-1)\) が\(\vec{0}\)となる実数\(t\)はなく、
\(\vec{a}=(t+2,t^2-k)\) が\(\vec{0}\) となるとき
\(t+2=0\), \(t^2-k=0\) より
\(t=-2\), \(k=4\)
\(k=4\)のとき①は
\(t^2+4t+4=0\)
\((t+2)^2=0\)
\(t=-2\)
内積=0 となる\(t\)は \(t=-2\) のみで、このとき \(\vec{a},\vec{b}\) は \(\vec{a}=\vec{0}\) だから垂直にならないため、\(k=4\) も適する。
したがって
\(0<k≦4\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→内積とベクトルの大きさ① back→なす角