(問題1)
\(y=x^4+2x^2+3\)の最小値を求めよ。
この問題にどうアプローチしますか?与えられた関数は\(x\)の4次関数なので微分(数Ⅱ)の知識がある方は微分をする方針で解くかもしれません。しかし与えられた関数をよく見ると、\(x^2\)の2次式であることがわかるので、\(x^2=t\)とおきかえれば2次関数に帰着させることができます。今回は後者の方針で解いていきたいと思います。
\(t=x^2\)・・・①とおくと、与式は
\(y=t^2+2t+3=(t+1)^2+2\) ・・・②だから
\(t=-1\)のとき最小値\(2\)としがちですが、はたして置き換えた②の\(t\)はすべての実数値をとるのでしょうか。答えは否で、①から\(t\)は、\(t≧0\) の値しかとらないことが分かります。このように置きかえをした場合、置きかえた文字のとりうる値に注意してください。
\(y=t^2+2t+3=(t+1)^2+2\) ・・・②だから
\(t=-1\)のとき最小値\(2\)としがちですが、はたして置き換えた②の\(t\)はすべての実数値をとるのでしょうか。答えは否で、①から\(t\)は、\(t≧0\) の値しかとらないことが分かります。このように置きかえをした場合、置きかえた文字のとりうる値に注意してください。
(解答)
\(x^2=t\)とおくと \(t≧0\)・・・(ア)で
与式は、\(y=t^2+2t+3=(t+1)^2+2\)・・・(イ)
(ア)の範囲で(イ)のグラフは以下の通り。
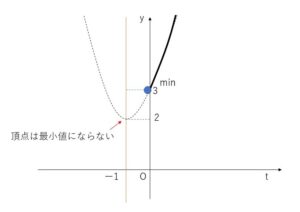
グラフより、最小値は\(t=0\)のとき\(3\)
このとき \(x^2=t=0\) より\(x=0\)
よって 最小値は\(3\) (\(x=0\))
(問題2)
関数 \(y=(x^2+2x)(x^2+2x+3)\)の最小値を求めよ。
こちらも4次関数です。微分しても解けますが面倒です。そこで\(x^2+2x\)という形が2回表れているので、置きかえして2次関数にします。こちらも置きかえたら値のとりうる範囲に注意です。
(解答)
\(t=x^2+2x=(x+1)^2-1\)とおくと \(t≧-1\)・・・①
\(t=x^2+2x=(x+1)^2-1\)とおくと \(t≧-1\)・・・①
関数は
\(y=t(t+3)=t^2+3t=(t+\displaystyle\frac{3}{2})^2-\displaystyle\frac{9}{4}\)・・・②
\(y=t(t+3)=t^2+3t=(t+\displaystyle\frac{3}{2})^2-\displaystyle\frac{9}{4}\)・・・②
②の軸\(t=-\displaystyle\frac{3}{2}\) は①の定義域より左側で、②のグラフは下に凸のグラフなので
最小値は\(t=-1\)のとき\(y=-2\)
最小値は\(t=-1\)のとき\(y=-2\)
このとき \(t=x^2+2x\) から
\(-1=x^2+2x\)
これを解いて \(x=-1\)
\(-1=x^2+2x\)
これを解いて \(x=-1\)
以上から,最小値は\(-2\) (\(x=-1\))
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。