三角形の形状 | 教えて数学理科

ベクトルに関する三角形の形状についての問題です。

(例題1)
(1)\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\overrightarrow{BC}\cdot\overrightarrow{CA}=\overrightarrow{CA}\cdot\overrightarrow{AB}\) を満たす\(△ABC\)はどのような三角形か。

(2)四角形\(ABCD\)と点\(O\)があり、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\), \(\overrightarrow{OD}=\vec{d}\) とおく。
\(\vec{a}+\vec{c}=\vec{b}+\vec{d}\) かつ \(\vec{a}\cdot\vec{c}=\vec{b}\cdot\vec{d}\) のとき、この四角形の形を調べよ。

(解答)
(1)

色々式変形できると思いますが、対称性に着目すると
左辺と中辺においては始点を\(A\)に、中辺と右辺においては始点を\(B\)に統一します。
(左辺と右辺では\(C\)に統一)

\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\overrightarrow{BC}\cdot\overrightarrow{CA}=\overrightarrow{CA}\cdot\overrightarrow{AB}\)　において

\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\overrightarrow{BC}\cdot\overrightarrow{CA}\) より
\(\overrightarrow{AB}\cdot(\overrightarrow{AC}-\overrightarrow{AB})=(\overrightarrow{AC}-\overrightarrow{AB})\cdot(-\overrightarrow{AC})\)
\(|\overrightarrow{AB}|^2=|\overrightarrow{AC}|^2\)
よって
\(|\overrightarrow{AB}|=|\overrightarrow{AC}|\)・・・①

\(\overrightarrow{BC}\cdot\overrightarrow{CA}=\overrightarrow{CA}\cdot\overrightarrow{AB}\) より
\(\overrightarrow{BC}\cdot(\overrightarrow{BA}-\overrightarrow{BC})=(\overrightarrow{BA}-\overrightarrow{BC})\cdot(-\overrightarrow{BA})\)
\(|\overrightarrow{BC}|^2=|\overrightarrow{BA}|^2\)
よって
\(|\overrightarrow{BC}|=|\overrightarrow{BA}|\)・・・②

①②から
\(|\overrightarrow{AB}|=|\overrightarrow{AC}|=|\overrightarrow{BC}|\)

したがって\(△ABC\)は正三角形。

(2)

四角形において対角線が互いに他を2等分するとき、平行四辺形になります。

\(\vec{a}+\vec{c}=\vec{b}+\vec{d}\)・・・③
\(\vec{a}\cdot\vec{c}=\vec{b}\cdot\vec{d}\)・・・④ において

③より
\(\displaystyle\frac{\vec{a}+\vec{c}}{2}=\displaystyle\frac{\vec{b}+\vec{d}}{2}\)

\(AC\)の中点と\(BD\)の中点が一致、つまり対角線が互いに他を2等分するので、四角形\(ABCD\)は平行四辺形。

また③より \(\vec{d}=\vec{a}+\vec{c}-\vec{b}\) を④に代入して
\(\vec{a}\cdot\vec{c}=\vec{b}\cdot(\vec{a}+\vec{c}-\vec{b})\)
\(\vec{a}\cdot\vec{c}-\vec{b}\cdot\vec{a}-\vec{b}(\vec{c}-\vec{b})=0\)
\(\vec{a}\cdot(\vec{c}-\vec{b})-\vec{b}(\vec{c}-\vec{b})=0\)
\((\vec{a}-\vec{b})\cdot(\vec{c}-\vec{b})=0\)
\(\overrightarrow{BA}\cdot\overrightarrow{BC}=0\)

\(|\overrightarrow{BA}|≠0\), \(|\overrightarrow{BC}|≠0\) だから
\(\angle B=90°\)

以上から、1つの内角が\(90°\)の平行四辺形になるので、四角形\(ABCD\)は長方形。

解答の\(\vec{d}\)消去と同様に、③から \(\vec{a},\vec{b},\vec{c}\) を消去して、4つの内角が\(90°\)になることを示してもよいです。

(例題2)
\(△OAB\)の辺\(OA,AB,BO\)のおのおのを \(t:(1-t)\) の比に内分する点をそれぞれ\(P,Q,R\)とする。ここで、\(t\)は \(0<t<1\) を満たす実数とする。

(1)\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) とするとき、\(\overrightarrow{PQ},\overrightarrow{PR}\) を \(t,\vec{a},\vec{b}\) を用いて表せ。
(2)\(\displaystyle\frac{|\overrightarrow{PQ}|}{|\overrightarrow{PR}|}=\displaystyle\frac{|\vec{b}|}{|\vec{a}|}\) が\(t\)の値によらず成り立つのは、\(△OAB\)がどのような三角形のときか。

(解答)
(1)

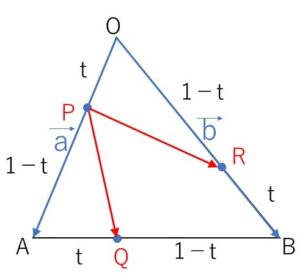
三角形形状　ベクトル

\(\overrightarrow{OP}=t\vec{a}\),　\(\overrightarrow{OQ}=(1-t)\vec{a}+t\vec{b}\),　\(\overrightarrow{OR}=(1-t)\vec{b}\) だから

\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}\)
\(=(1-t)\vec{a}+t\vec{b}-t\vec{a}\)
\(=(1-2t)\vec{a}+t\vec{b}\)

\(\overrightarrow{PR}=\overrightarrow{OR}-\overrightarrow{OP}\)
\(=(1-t)\vec{b}-t\vec{a}\)
\(=-t\vec{a}+(1-t)\vec{b}\)

(2)

条件式は\(t\)の恒等式です。
係数比較か数値代入(十分性の確認が必要)で解きます。解答では数値代入法にします。

\(\displaystyle\frac{|\overrightarrow{PQ}|}{|\overrightarrow{PR}|}=\displaystyle\frac{|\vec{b}|}{|\vec{a}|}\) より

\(|\vec{a}|^2|\overrightarrow{PQ}|^2=|\vec{b}|^2|\overrightarrow{PR}|^2\)
\(|\vec{a}|^2|(1-2t)\vec{a}+t\vec{b}|^2=|\vec{b}|^2|-t\vec{a}+(1-t)\vec{b}|^2\)

\(|\vec{a}|^2\{(1-2t)^2|\vec{a}|^2+2t(1-2t)\vec{a}\cdot\vec{b}+t^2|\vec{b}|^2\}\)\(=|\vec{b}|^2\{t^2|\vec{a}|^2-2t(1-t)\vec{a}\cdot\vec{b}+(1-t)^2|\vec{b}|^2\}\)・・・①

\(t=0,\displaystyle\frac{1}{2},1\) 辺りが代入する値の候補です。

①は\(t\)についての恒等式となる。

\(t=0\)を代入して
\(|\vec{a}|^4=|\vec{b}|^4\)
よって
\(|\vec{a}|=|\vec{b}|\)・・・②

\(t=\displaystyle\frac{1}{2}\) を代入すると
\(\displaystyle\frac{1}{4}|\vec{a}|^2|\vec{b}|^2=|\vec{b}|^2(\displaystyle\frac{1}{4}|\vec{a}|^2-\displaystyle\frac{1}{2}\vec{a}\cdot\vec{b}+\displaystyle\frac{1}{4}|\vec{b}|^2)\)

②から
\(\displaystyle\frac{1}{4}|\vec{a}|^2=\displaystyle\frac{1}{4}|\vec{a}|^2-\displaystyle\frac{1}{2}\vec{a}\cdot\vec{b}+\displaystyle\frac{1}{4}|\vec{a}|^2\)
\(\vec{a}\cdot\vec{b}=\displaystyle\frac{1}{2}|\vec{a}|^2\)
\(|\vec{a}||\vec{a}|\cos\angle O=\displaystyle\frac{1}{2}|\vec{a}|^2\)
\(\cos\angle O=\displaystyle\frac{1}{2}\)
よって
\(\angle O=60°\)・・・③

②③より \(OA=OB\), \(\angle O=60°\) となるから、\(△OAB\)は正三角形である。

最後に逆の確認、
「\(△OAB\)が正三角形　→　\(\displaystyle\frac{|\overrightarrow{PQ}|}{|\overrightarrow{PR}|}=\displaystyle\frac{|\vec{b}|}{|\vec{a}|}\)」
を示します。内積を用いて、\(|\overrightarrow{PQ}|,|\overrightarrow{PR}|\) を計算してもよいですが、図形的に解いた方が早いです。

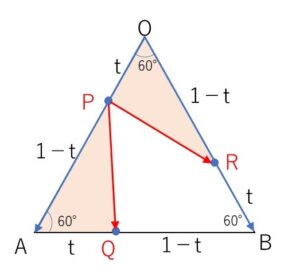
三角形形状ベクトル2

逆に\(△OAB\)が正三角形であるとき
\(t\)の値によらず、\(△OPR≡△AQP\)となるから \(|\overrightarrow{PR}|=|\overrightarrow{PQ}|\)

また \(|\vec{a}|=|\vec{b}|\)

よって
\(\displaystyle\frac{|\overrightarrow{PQ}|}{|\overrightarrow{PR}|}=\displaystyle\frac{|\vec{b}|}{|\vec{a}|}(=1)\) が\(t\)の値によらず成り立つ。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→チェバ,メネラウスの定理とベクトル　 back→軌跡・領域⑤(ベクトルの選択)