空間ベクトルの平行条件について見ていきます。
・空間ベクトルの平行
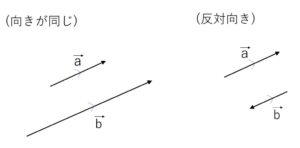
\(\vec{0}\)でない2つのベクトル \(\vec{a},\vec{b}\)の向きが同じか、反対向きであるとき、\(\vec{a}\)と\(\vec{b}\)は平行であるといいます。
よってベクトルの実数倍の定義からベクトルの平行条件は次の通りです。
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
\(\vec{a}/\!/\vec{b}\) \(⇔\) \(\vec{a}=k\vec{b}\) となる実数\(k\)が存在する
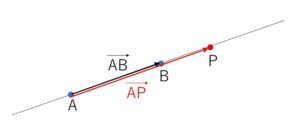
また異なる2点\(A,B\)に対して、点\(P\)が直線\(AB\)上にある(\(A,B,P\)が1直線上にある)条件は、\(\overrightarrow{AB}/\!/\overrightarrow{AP}\) または \(\overrightarrow{AP}=\vec{0}\) となるので
点\(P\)が直線\(AB\)上にある \(⇔\) \(\overrightarrow{AP}=k\overrightarrow{AB}\) となる実数\(k\)が存在する
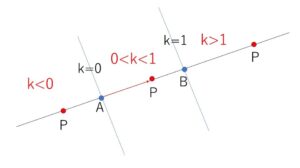
なお、\(k\)の値に対応した点\(P\)の位置は次の通りです。
(例題1)
\(A(1,2,4)\), \(B(2,5,6)\), \(C(x,y,10)\) の3点が同一直線上にあるとき、\(x\)と\(y\)の値を求めよ。
(解答)
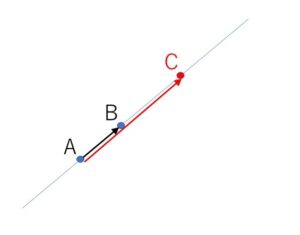
\(k\)を実数として
\(\overrightarrow{AC}=k\overrightarrow{AB}\)
\((x-1,y-2,6)=k(1,3,2)\)
各成分を比較して
\(x-1=k\)・・・①
\(y-2=3k\)・・・②
\(6=2k\)・・・③
③より\(k=3\)
①②より
\(x=4\), \(y=11\)
(例題2)
4点 \(A(1,-2,-3)\), \(B(2,1,1)\), \(C(-1,-3,2)\), \(D(3,-4,-1)\) がある。線分\(AB,AC,AD\)を3辺にもつ平衡六面体の他の頂点の座標を求めよ。
(解答)
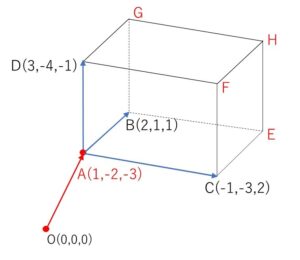
図のように残りの頂点を\(E,F,G,H\)とする。
\(\overrightarrow{AB}=(1,3,4)\)
\(\overrightarrow{AC}=(-2,-1,5)\)
\(\overrightarrow{AD}=(2,-2,2)\)
より
\(\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}\)
\(=(1,-2,-3)+(1,3,4)+(-2,-1,5)\)
\(=(0,0,6)\)
\(\overrightarrow{OF}=\overrightarrow{OA}+\overrightarrow{AC}+\overrightarrow{AD}\)
\(=(1,-2,-3)+(-2,-1,5)+(2,-2,2)\)
\(=(1,-5,4)\)
\(\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AD}\)
\(=(1,-2,-3)+(1,3,4)+(2,-2,2)\)
\(=(4,-1,3)\)
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\)
\(=(1,-2,-3)+(1,3,4)+(-2,-1,5)+(2,-2,2)\)
\(=(2,-2,8)\)
したがって他の頂点の座標は
\((0,0,6)\), \((1,-5,4)\), \((4,-1,3)\), \((2,-2,8)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→1次独立(空間ベクトル) back→空間ベクトルの成分