空間ベクトルの内積について見ていきます。
・空間ベクトルの内積
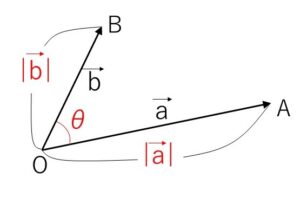
平面ベクトルと同じように、\(\vec{0}\)でない2つのベクトル \(\vec{a},\vec{b}\) のなす角を\(θ\) (\(0°≦θ≦180°\)) として、内積 \(\vec{a}\cdot\vec{b}\) を次のように定義します。
\(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cosθ\)
また、\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のときは、\(\vec{a}\cdot\vec{b}=0\) とします。
そして、\(\vec{a}=(a_1,a_2,a_3)\), \(\vec{b}=(b_1,b_2,b_3)\) と成分表示したときの内積は、平面ベクトルの場合に\(z\)成分の項を追加した式となります。
\(\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3\)
証明は平面ベクトルと同様に余弦定理を考えます。
(証明)
(i)\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
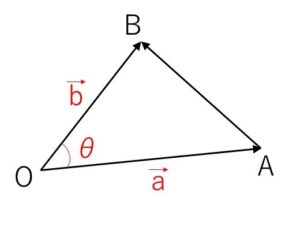
\(0°<θ<180°\) のとき三角形\(OAB\)が存在するので余弦定理より
\(AB^2=OA^2+OB^2-2OA\cdot OB\cosθ\)
(\(θ=0°,180°\)でも成立する)
\(OA\cdot OB\cosθ=\vec{a}\cdot\vec{b}\) だから
\(2\vec{a}\cdot\vec{b}=OA^2+OB^2-AB^2\)
\(2\vec{a}\cdot\vec{b}=(a_1^2+a_2^2+a_3^2)+(b_1^2+b_2^2+b_3^2)\)\(-\{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2\}\)
\(2\vec{a}\cdot\vec{b}=2a_1b_1+2a_2b_2+2a_3b_3\)
したがって
\(\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3\)・・・①
(ii)\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のとき
①の両辺は\(0\)になるので成立。
・内積の演算
内積の定義や、成分表示による計算により平面ベクトルのときと同様に次のことが成り立ちます。
(1)\(\vec{a}\cdot\vec{a}=|\vec{a}|^2\) (ベクトルの2乗)
(2)\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\) (交換法則)
(3)\((\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}\) (分配法則)
(\(\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}\))
(4)\((k\vec{a})\cdot\vec{b}=\vec{a}\cdot(k\vec{b})=k(\vec{a}\cdot\vec{b})\) (\(=k\vec{a}\cdot\vec{b}\)) (\(k\)は実数)
(1)の大きさに2乗になる式には注意しましょう。
・内積と平行・垂直
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき、\(0°≦θ≦180°\) では
\(-1≦\cosθ≦1\) なので、辺々に\(|\vec{a}||\vec{b}|\) を掛けて
\(-|\vec{a}||\vec{b}|≦\vec{a}\cdot\vec{b}≦|\vec{a}||\vec{b}|\) (\(\vec{a},\vec{b}\)が\(\vec{0}\)のときも成り立つ)
等号は
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
右側については \(θ=0°\) のとき
左側については \(θ=180°\) のとき
\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のときは全ての辺が\(0\)になり成立します。
ここで改めて、\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) とすると
\(θ=90°\) のとき \(\cosθ=0\)
\(θ=0°,180°\) のとき \(\cosθ=±1\) なので
垂直については成分表示による内積もまとめると、次のことが成り立ちます。
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
(垂直条件) \(\vec{a} \perp \vec{b}\) \(⇔\) \(\vec{a}\cdot\vec{b}=0\) \(⇔\) \(a_1b_1+a_2b_2+a_3b_3=0\)
(平行条件) \(\vec{a} /\!/ \vec{b}\) \(⇔\) \(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|または-|\vec{a}||\vec{b}|\)
詳しくは →(平面ベクトル内積) を参照してください。
(例題)
1辺の長さが\(1\)の正四面体\(OABC\)において、2辺\(AB,OC\)の中点をそれぞれ\(M,N\)とする。\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とするとき、次の問いに答えよ。
(1)\(\overrightarrow{NM},\overrightarrow{NB}\) を\(\vec{a},\vec{b},\vec{c}\) を用いて表せ。
(2)\(\overrightarrow{NM}\) と \(\overrightarrow{NB}\) の内積を求めよ。
(解答)
(1)
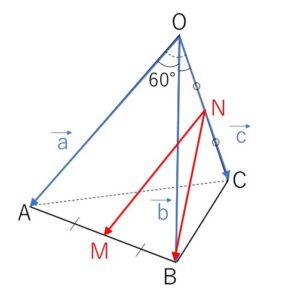
\(\overrightarrow{OM}=\overrightarrow{OA}+\displaystyle\frac{1}{2}\overrightarrow{AB}\)
\(=\overrightarrow{OA}+\displaystyle\frac{1}{2}(\overrightarrow{OB}-\overrightarrow{OA})\)
\(=\displaystyle\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})\)
\(=\displaystyle\frac{1}{2}\vec{a}+\displaystyle\frac{1}{2}\vec{b}\)
\(\overrightarrow{ON}=\displaystyle\frac{1}{2}\vec{c}\)
よって
\(\overrightarrow{NM}=\overrightarrow{OM}-\overrightarrow{ON}\)
\(=\displaystyle\frac{1}{2}(\vec{a}+\vec{b}-\vec{c})\)
\(\overrightarrow{NB}=\overrightarrow{OB}-\overrightarrow{ON}\)
\(=\displaystyle\frac{1}{2}(2\vec{b}-\vec{c})\)
(2)
あとは(1)の結果から計算していきます。
\(\overrightarrow{NM}\cdot\overrightarrow{NB}\)
\(=\displaystyle\frac{1}{2}(\vec{a}+\vec{b}-\vec{c})\cdot\displaystyle\frac{1}{2}(2\vec{b}-\vec{c})\)
\(=\displaystyle\frac{1}{4}(\vec{a}+\vec{b}-\vec{c})\cdot(2\vec{b}-\vec{c})\)・・・①
ここで、\(|\vec{a}|^2=|\vec{b}|^2=|\vec{c}|^2=1\)
また、\(\vec{a}\cdot\vec{b}=1\cdot1\cdot\cos60°=\displaystyle\frac{1}{2}\)
同様に、\(\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=\displaystyle\frac{1}{2}\)
よって①は
\(\displaystyle\frac{1}{4}(1+2-1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{2}+1)\)
\(=\displaystyle\frac{1}{2}\)
したがって
\(\overrightarrow{NM}\cdot\overrightarrow{NB}=\displaystyle\frac{1}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の面積 back→1次独立(空間ベクトル)