ベクトルの掛け算(内積)について見ていきます。
内積は平面ベクトル,空間ベクトルどちらにも存在します。外積は空間ベクトルにおけるもので、高校の範囲外の内容です。
・ベクトルの内積
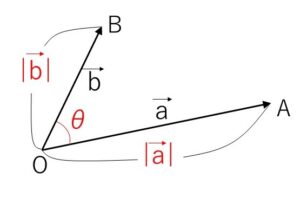
\(\vec{0}\)でない2つのベクトル\(\vec{a},\vec{b}\) に対して点\(O\)を始点として、\(\vec{a}=\overrightarrow{OA}\), \(\vec{b}=\overrightarrow{OB}\) となるように点\(A,B\)をとります。このとき、\(\angle AOB\) の大きさ\(θ\) (ただし \(0°≦θ≦180°\) になるようにとる) を \(\vec{a}\), \(\vec{b}\) のなす角 といいます。
このとき \(\vec{a}\)と\(\vec{b}\) の内積 \(\vec{a}\cdot\vec{b}\) を次のように定義します。
\(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cosθ\)
そして、\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のときは、\(\vec{a}\cdot\vec{b}=0\) と定めます。
またベクトルの掛け算を定義する理由は、
・内積と大きさが分かっている or 成分により計算できる(次回参照) 場合に、\(\cosθ\) の値が分かるのでなす角が分かる
・ベクトルの等式の両辺にベクトルを掛け算して式変形できる
・ベクトルの絶対値(大きさ)を内積により計算できる
など有用なことがあるからです。
また内積の定義から
\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\) (交換法則)
\(\vec{a}\) と \(\vec{a}\) のなす角は\(0°\) (重なる)だから
\(\vec{a}\cdot\vec{a}=|a|^2\) (ベクトルの2乗は大きさの2乗)
どちらも\(\vec{0}\)となるときを含めて成り立ちます。
・内積と平行・垂直
なす角\(θ\)による内積の変化について考えます。
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\)として、\(0°≦θ≦180°\) のとき
\(-1≦\cosθ≦1\) だから、辺々に \(|\vec{a}||\vec{b}|\) を掛けて
\(-|\vec{a}||\vec{b}|≦|\vec{a}||\vec{b}|\cosθ≦|\vec{a}||\vec{b}|\)
\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のときも含めて、次の不等式が成り立ちます。
\(-|\vec{a}||\vec{b}|≦\vec{a}\cdot\vec{b}≦|\vec{a}||\vec{b}|\)
等号は
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
右辺については、\(θ=0°\) のとき
左辺については、\(θ=180°\) のとき
また、\(\vec{a}=\vec{0}\) または \(\vec{b}=\vec{0}\) のときも全ての辺が\(0\)になるために成立します。
ここで \(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) として、\(θ\)によって内積を分類すると
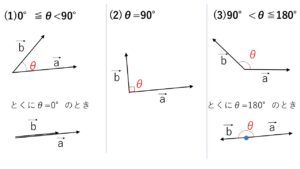
(1)\(0°≦θ<90°\) のとき
\(\cosθ>0\) より \(\vec{a}\cdot\vec{b}>0\)
とくに \(θ=0°\) のとき
\(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\) であり
\(\vec{a},\vec{b}\) は同じ向きに平行になります。
(2)\(θ=90°\) のとき
このとき\(\vec{a},\vec{b}\) は垂直であるといい、\(\vec{a}\perp\vec{b}\) で表します。
内積については \(\cosθ=0\) より \(\vec{a}\cdot\vec{b}=0\)
(3)\(90°<θ≦180°\) のとき
\(\cosθ<0\) より \(\vec{a}\cdot\vec{b}<0\)
とくに \(θ=180°\) のとき
\(\vec{a}\cdot\vec{b}=-|\vec{a}||\vec{b}|\) であり
\(\vec{a},\vec{b}\) は反対向きに平行になります。
まとめると
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) のとき
\(\vec{a}\perp\vec{b}\) \(⇔\) \(\vec{a}\cdot\vec{b}=0\)
\(\vec{a}/\!/\vec{b}\) \(⇔\) \(\vec{a}\cdot\vec{b}=|a||b|または-|a||b|\)
・内積の図形的意味
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\) とします。
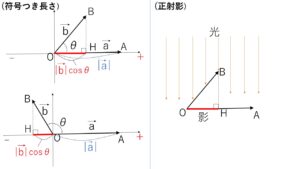
内積の定義から
\(\vec{a}\cdot\vec{b}=|\vec{a}|×|\vec{b}|\cosθ=OA×(OB\cosθ)\)
(\(OA,OB>0\))
点\(B\)から直線\(OA\)に垂線を下してその足を\(H\)とし、
ここで\(\overrightarrow{OA}\)を正の向きとした符号つきの長さを考えると、\(OB\cosθ\) は符号つきの長さになるので、それを\(OH\)とすると
\(\vec{a}\cdot\vec{b}=OA×OH\)
また、\(OH\)は上から直線\(OA\)に垂直な光線をあててできる線分\(OB\)の影になるので、\(\overrightarrow{OH}\) を 「\(\overrightarrow{OB}\)の直線\(OA\)上への正射影」とよびます。
したがってベクトルの内積は、「\(OA\)に映した正射影の大きさと\(OA\)の大きさの符号つきの積」と捉えることができます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内積(成分表示) back→ベクトルの1次独立と分解