ベクトルのなす角、垂直なベクトルに関する問題について見ていきます。
(例題1)
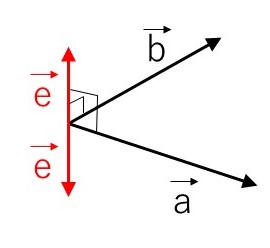
2つのベクトル \(\vec{a}=(2,1,3)\), \(\vec{b}=(1,-1,0)\) の両方に垂直な単位ベクトルを求めよ。
(解答)
大きさ\(1\)である条件 \(x^2+y^2+z^2=1\) も忘れずに。
求める単位ベクトルを \(\vec{e}=(x,y,z)\) とおくと
\(\vec{a}\cdot\vec{e}=0\), \(\vec{b}\cdot\vec{e}=0\) より
\(2x+y+3z=0\)・・・①
\(x-y=0\)・・・②
また\(|\vec{e}|=1\) だから
\(x^2+y^2+z^2=1\)・・・③
②より \(y=x\)・・・④
①に代入して \(2x+x+3z=0\)
よって\(z=-x\)・・・⑤
③に④⑤を代入して
\(x^2+x^2+(-x)^2=1\)
\(x=±\displaystyle\frac{1}{\sqrt{3}}\)
④⑤より求める単位ベクトルは
\((\displaystyle\frac{1}{\sqrt{3}},\displaystyle\frac{1}{\sqrt{3}},-\displaystyle\frac{1}{\sqrt{3}})\), \((-\displaystyle\frac{1}{\sqrt{3}},-\displaystyle\frac{1}{\sqrt{3}},\displaystyle\frac{1}{\sqrt{3}})\)
(例題2)
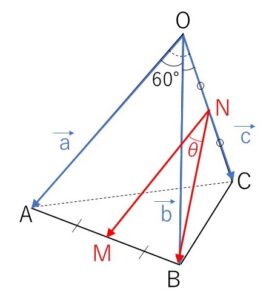
1辺の長さが\(1\)の正四面体\(OABC\)において、2辺\(AB,OC\)の中点をそれぞれ\(M,N\)とする。\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{c}\) とするとき、次の問いに答えよ。
(1)\(\overrightarrow{NM},\overrightarrow{NB}\) を\(\vec{a},\vec{b},\vec{c}\) を用いて表せ。
(2)\(\overrightarrow{NM}\) と \(\overrightarrow{NB}\) の内積を求めよ。
(3)\(\angle BNM=θ\) とするとき、\(\cosθ\) の値を求めよ。
(解答)
(1)
\(\overrightarrow{OM}=\displaystyle\frac{1}{2}(\vec{a}+\vec{b})\)
\(\overrightarrow{ON}=\displaystyle\frac{1}{2}\vec{c}\)
よって
\(\overrightarrow{NM}=\overrightarrow{OM}-\overrightarrow{ON}\)
\(=\displaystyle\frac{1}{2}(\vec{a}+\vec{b}-\vec{c})\)
\(\overrightarrow{NB}=\overrightarrow{OB}-\overrightarrow{ON}\)
\(=\displaystyle\frac{1}{2}(2\vec{b}-\vec{c})\)
(2)
\(|\vec{a}|=|\vec{b}|=|\vec{c}|=1\)
また、正四面体の各面は正三角形だから
\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}=\vec{c}\cdot\vec{a}=1\cdot1\cdot\cos60°=\displaystyle\frac{1}{2}\)
よって
\(\overrightarrow{NM}\cdot\overrightarrow{NB}\)
\(=\displaystyle\frac{1}{2}(\vec{a}+\vec{b}-\vec{c})\cdot\displaystyle\frac{1}{2}(2\vec{b}-\vec{c})\)
\(=\displaystyle\frac{1}{4}(\vec{a}+\vec{b}-\vec{c})\cdot(2\vec{b}-\vec{c})\)
\(=\displaystyle\frac{1}{4}(1+2-1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{2}+1)\)
\(=\displaystyle\frac{1}{2}\)
(3)
内積は(2)で求めたので、大きさを2乗を利用して求めていきます。
\(|\overrightarrow{NM}|^2\)
\(=|\displaystyle\frac{1}{2}(\vec{a}+\vec{b}-\vec{c})|^2\)
\(=\displaystyle\frac{1}{4}(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2+2\vec{a}\cdot\vec{b}-2\vec{b}\cdot\vec{c}-2\vec{c}\cdot\vec{a})\)
\(=\displaystyle\frac{1}{4}(1+1+1+1-1-1)\)
\(=\displaystyle\frac{1}{2}\)
\(|\overrightarrow{NB}|^2\)
\(=|\displaystyle\frac{1}{2}(2\vec{b}-\vec{c})|^2\)
\(=\displaystyle\frac{1}{4}(4|\vec{b}|^2-4\vec{b}\cdot\vec{c}+|\vec{c}|^2)\)
\(=\displaystyle\frac{1}{4}(4-2+1)\)
\(=\displaystyle\frac{3}{4}\)
よって
\(\overrightarrow{NM}\cdot\overrightarrow{NB}=|\overrightarrow{NM}||\overrightarrow{NB}|\cosθ\) より
\(\displaystyle\frac{1}{2}=\displaystyle\frac{1}{\sqrt{2}}\cdot\displaystyle\frac{\sqrt{3}}{2}\cosθ\)
したがって
\(\cosθ=\sqrt{\displaystyle\frac{2}{3}}\)
(例題3)
空間の2点\(P,Q\)と原点\(O\)について
\(\overrightarrow{OP}=(2\cos t,2\sin t,1)\), \(\overrightarrow{OQ}=(-\sin3t,\cos3t,-1)\)
とする。ただし、\(-180°≦t≦180°\) とする。
(1)\(|\overrightarrow{OP}|,|\overrightarrow{OQ}|,\) 内積 \(\overrightarrow{OP}\cdot\overrightarrow{OQ}\) を求めよ。
(2)\(\overrightarrow{OP}\)と\(\overrightarrow{OQ}\)のなす角が\(0°\)以上\(90°\)以下となる\(t\)の範囲を求めよ。
(解答)
(1)
\(|\overrightarrow{OP}|=\sqrt{4\cos^2t+4\sin^2t+1}\)\(=\sqrt{5}\)
\(|\overrightarrow{OQ}|=\sqrt{\sin^23t+\cos^23t+1}\)\(=\sqrt{2}\)
\(\overrightarrow{OP}\cdot\overrightarrow{OQ}\)
\(=-2\cos t\sin3t+2\sin t\cos3t-1\)
(加法定理に備えて掛ける順番を入れ替える)
\(=-2(\sin3t\cos t-\cos3t\sin t)-1\)
(加法定理の展開の逆の操作を行って)
\(=-2\sin(3t-t)-1\)
\(=-2\sin2t-1\)
(2)
\(\overrightarrow{OP}\)と\(\overrightarrow{OQ}\)のなす角を\(θ\)とすれば
\(\overrightarrow{OP}\cdot\overrightarrow{OQ}=|\overrightarrow{OP}||\overrightarrow{OQ}|\cosθ\)
(1)より
\(-2\sin2t-1=\sqrt{5}\cdot\sqrt{2}\cosθ\)
よって
\(\cosθ=-\displaystyle\frac{1}{\sqrt{10}}(2\sin2t+1)\)
なす角が\(0°\)以上\(90°\)以下だから
\(0≦-\displaystyle\frac{1}{\sqrt{10}}(2\sin2t+1)≦1\)
\(-\sqrt{10}≦2\sin2t+1≦0\)
\(-\displaystyle\frac{1+\sqrt{10}}{2}≦\sin2t≦-\displaystyle\frac{1}{2}\)
よって左側の不等式は常に成立します。
ここで、\(-\displaystyle\frac{1+\sqrt{10}}{2}<-1\) より
\(-\displaystyle\frac{1+\sqrt{10}}{2}≦\sin2t\) は\(t\)によらず成立。
よって
\(\sin2t≦-\displaystyle\frac{1}{2}\) を満たす\(t\)を考えると
\(-360°≦2t≦360°\) より
\(-150°≦2t≦-30°\), \(210°≦2t≦330°\)
したがって求める\(t\)の範囲は
\(-75°≦t≦-15°\), \(105°≦t≦165°\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルの大きさ back→三角形の面積